16.4 Codifica differenziale
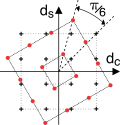
Se la portante con cui si effettua la demodulazione presenta un errore di fase, il piano dell’inviluppo complesso subisce una rotazione, producendo decisioni sistematicamente
errate a causa dello spostamento dei punti di costellazione ottenuti campionando le c.a. di b.f. (pallini rossi) rispetto a quelli che si otterrebbero nel caso di demodulazione
coerente (crocette nere). Per rimediare al problema, si può estendere il principio della codifica
differenziale (espresso a pag.
1 per segnali di banda base) al caso delle modulazioni numeriche, rendendo la decisione su quale punto di costellazione sia stato ricevuto indipendente dalla fase della portante di demodulazione, ma dipendente invece dalla fase dell’inviluppo complesso osservata
per il simbolo precedente. Ciò si realizza modificando il criterio con cui sono determinati i punti di costellazione da trasmettere, scegliendoli ora in funzione
di una coppia di simboli consecutivi, anziché di uno solo.
16.4.1 Modulazione DBPSK
Per illustrare la tecnica, procediamo con un esempio relativo al caso di trasmissione
bpsk della sequenza
xk = 001011011010010 e mostriamo come la codifica differenziale consenta di neutralizzare un errore di fase di
π.
La fig.
16.26, simile a quella a pag.
1, mostra la sequenza delle operazioni necessarie, e che consistono nel trasformare il messaggio binario
xk in quello
yk in base alla relazione
xk = 001011011010010
yk = 001101101100011
zk = ⁄ 01011011010010
(in cui l’operatore
⊕ rappresenta un
or esclusivo), e quindi effettuare la modulazione
bpsk di
yk anziché di
xk. Dal lato ricevente, il segnale
bpsk viene demodulato ottenendo la sequenza
ŷk, che viene a sua volta trasformata in
zk in base all’espressione
che, in assenza di errori (ossia se
ŷk = yk per tutti i
k), permette di ottenere nuovamente i valori del messaggio originario
xk a partire dalla sequenza
zk, come la figura del riquadro precedente consente di verificare tramite un esempio.
Se assumiamo ora di rappresentare lo zero con una fase nulla, e l’uno con una fase di
π, possiamo riscrivere la
(21.33) come
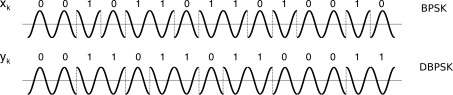
e ponendo per semplicità il periodo di bit pari ad un ciclo di portante, possiamo confrontare in fig.
16.27 la forma d’onda
bpsk associata alla sequenza originaria
xk, con quella ottenibile utilizzando nella
(21.50) yk anziché
xk ed indicata come
dbpsk, in cui la
d sta appunto per
differenziale.
Pertanto quando il demodulatore
bpsk di fig.
16.26 riceve il segnale
dbpsk, in assenza di errori si produce in uscita la sequenza
yk, e quindi il circuito mostrato realizza l’operazione
zk = ŷk ⊕ ŷk − 1, permettendo di ottenere la sequenza originaria. Verifichiamo ora che il segnale di partenza viene recuperato anche se la portante di demodulazione presenta un errore di fase di
π, tale da causare
l’inversione della forma d’onda e quindi di tutti i bit decodificati, producendo un messaggio
ŷk = yk = 110010010011100 (la sopralineatura rappresenta l’inversione logica). Infatti, applicando la
(21.49) alla sequenza
ŷk = yk si ottiene di nuovo la sequenza originaria, dato che
a ⊕ b = a ⊕ b.
D’altra parte lo schema di fig.
16.26 non è l’unico possibile, osservando che la sequenza
xk può anche essere derivata
direttamente dall’esame visivo della forma d’onda
dbpsk, in quanto i bit della sequenza
yk cambiano nel caso in cui il corrispondente bit di
xk è un uno, mentre
non cambiano se è uno zero, e dunque lo stesso accade per il segno della forma d’onda
dbpsk. Il demodulatore può essere dunque sostituito da uno in fase e quadratura, in modo da calcolare la fase a partire dalle c.a. di b.f. come
φ = arctan dsdc, e quindi determinare la sequenza
xk in base alle
variazioni di fase, senza dover applicare la
(21.49), consentendo di applicare il principio anche in presenza di errori di fase qualsiasi, e non solo pari a
π.
Esaminiamo ora cosa accade in presenza di errori: supponiamo di ricevere un messaggio
yk = 000101101100011, in cui il terzo bit (sottolineato) è errato. Calcolando
zk = ŷk ⊕ ŷk − 1 questa volta si ottiene
zk = ⁄ 00111011010010 che risulta uguale a
xk tranne che nel terzo e quarto bit. Infatti, dato che
zk dipende dagli indici
k e
k − 1 di
y, l’effetto dell’errore non si propaga oltre il bit successivo a quello errato. Dato quindi che ad ogni errore del decisore si ottengono due bit errati anziché uno, a prima vista possiamo dire che a parità di
Eb⁄N0, il
dbpsk è affetto da un tasso di errore
circa doppio di quello del
bpsk. Una analisi più approfondita (che omettiamo) fornisce l’espressione
che equivale ad un peggioramento di prestazioni di circa 1 dB rispetto al
bpsk, ed il cui andamento è riportato a pag.
1.
Il concetto di codifica differenziale può essere facilmente esteso al caso di
l-psk, semplicemente mettendo in corrispondenza le configurazioni di bit previste dal codice di Gray con rotazioni di fase
Δθ (tra simboli successivi) contigue, come esemplificato nella tabella che segue per
L = 4(), ovvero nel caso della modulazione
dqpsk. L’inviluppo complesso di tale segnale assumerà quindi, negli istanti di simbolo, valori
| xk − 1xk |
Δθ |
| 00 |
0 |
| 01 |
π⁄2 |
| 11 |
π |
| 10 |
− π⁄2 |
la cui fase dipende dalla fase del simbolo precedente, incrementata del
Δθ mostrato in tabella, consentendo la corretta ricezione anche in presenza di una portante di demodulazione affetta da errori di fase multipli di
π2. Anche qui se (a causa del rumore) si verifica un errore di ricezione, questo si propaga anche al simbolo successivo.
Anche nel caso del qam si può applicare una forma di codifica differenziale, ma lo schema di corrispondenza tra gruppi di bit e punti della costellazione è più complesso, e non viene qui trattato.
Infine, la modulazione differenziale può essere proficuamente sfruttata nella trasmissione
ofdm (§
16.8.8), al fine di evitare la necessità di equalizzazione.