16.9 Sistemi a spettro espanso
In questa tecnica di modulazione la stessa banda di frequenze è utilizzata contemporaneamente da più trasmissioni differenti, che non interferiscono tra loro grazie all’uso di forme d’onda mutuamente ortogonali; ciò avviene adottando una opportuna
trasformazione del messaggio da trasmettere, in modo che questo occupi una banda molto maggiore di quella originaria, e sulla manipolazione inversa in ricezione. Il peculiare aumento della banda occupata è indicato con il termine di
spread spectrum, e la tecnica di trasmissione risultante prende anche il nome di multiplazione a divisione di codice
o
cdm (
code division multiplex).
Sebbene la doppia operazione di spreading/despreading non produca nessun vantaggio effettivo nei riguardi delle prestazioni ottenibili qualora la ricezione sia disturbata dalla sola presenza di rumore additivo gaussiano, si ottengono invece i seguenti altri benefici:
- altre trasmissioni e/o disturbi a banda stretta che occupano la stessa regione di frequenza occupata dal segnale espanso causano una potenza interferente ridotta;
- la densità spettrale del segnale trasmesso può confondersi con quella del rumore, rendendo la trasmissione stessa poco rilevabile da parte di soggetti ostili;
- per conoscere il contenuto della trasmissione occorre poter riprodurre in ricezione una esatta replica della trasformazione attuata.
16.9.1 Sequenze pseudo-casuali
La trasformazione che produce l’espansione spettrale si basa sull’utilizzo di una sequenza cosiddetta
pseudo-noise o
pn (§
16.9.3), ovvero le cui caratteristiche statistiche
si avvicinano a quelle di un rumore stazionario bianco e cioè a valori incorrelati, tranne che questi non sono casuali ma
deterministici, in modo che la loro ripetizione ciclica rende la sequenza
pn riproducibile dal lato ricevente. La fig.
16.46-a) mostra una parte di un possibile segnale dati
p(t) pseudo casuale, bipolare, di durata
L ⋅ Tp,
la cui espressione può essere posta nella forma
con
θ v.a. uniforme tra
± Tp⁄2, basata sulla ripetizione di impulsi
nrz bipolari
g(t) = rectTp(t) di durata
Tp con polarità stabilita dagli
L valori
ak, scelti pari a
±1 in modo da avvicinarsi alle condizioni
- media nulla e varianza unitaria, cioè mA = 0, σ2A = 1;
- una autocorrelazione Ra(n) la più piccola possibile con n ≠ 0 , mimando così la proprietà di indipendenza statistica.
Al §
7.7.4 abbiamo mostrato che un segnale simile a
p(t) ed espresso dalla
(21.70), nel caso in cui gli
ak siano v.a. indipendenti a media nulla, presenta uno spettro di densità di potenza
rappresentato in fig.
16.46-b), e per il quale la frequenza
Wp = 1Tp ne approssima l’occupazione di banda: prendiamo dunque questo risultato come una accettabile approssimazione per
p(t). Dalla
(21.71) consegue che l’autocorrelazione di
p(t) si esprime come
mostrata in fig.
16.46-c), e che appunto si azzera per
τ ≥ Tp. Sebbene le sequenze pseudo-noise utilizzate realmente (§
16.9.3) non aderiscano esattamente a queste caratteristiche, vi si avvicinano in modo soddisfacente per gli scopi delle telecomunicazioni.
L’estensione temporale Tp di un simbolo di p(t) è indicata come periodo di chip, e ci si riferisce ai suoi simboli come chip, per distinguerli dai bit; pertanto, la frequenza fp = Wp = 1⁄Tp è detta chip rate.
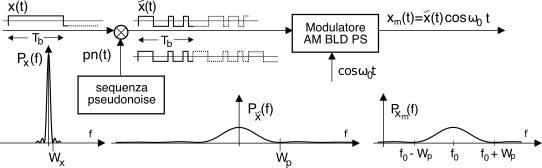
16.9.2 Modulazione per sequenza diretta
Ottiene l’espansione spettrale eseguendo il prodotto
x̃(t) = x(t) pn(t) tra un segnale di banda base
x(t) e la ripetizione ciclica del segnale
pn pn(t) = ∑∞i = −∞ p(t − iLTp), con il risultato di effettuare una modulazione
am-bld-ps; l’operazione nel suo insieme prende il nome di
Direct Sequence Spread Spectrum (o
dsss).
Sebbene l’effetto di espansione spettrale sia valido per
x(t) qualsiasi, affrontiamo l’analisi con riferimento ad un segnale
x(t) numerico binario
nrz antipodale ossia polare, il cui periodo di bit
Tb ≫ Tp ne determina una densità di potenza
Px(f) del tipo di
(21.71) ma con banda
Wx ≪ Wp. La fig.
16.48 illustra la situazione, facendo anche notare come scegliendo
Tb = LTp e moltiplicando i bit del messaggio per la sequenza di chip della
pn si ottiene di fatto una
sequenza di sequenze pn, ognuna con segno invertito o meno a seconda del valore dei singoli bit del messaggio, e con una banda che è quella di un segnale dati a frequenza
fp = Wp ≫ fb. Osserviamo che il segnale
allargato x̃(t) è così chiamato anche perché la potenza
Px̃ è la stessa
Px di
x(t), che ora risulta però
spalmata sulla banda
Wp di
pn(t).
L’effetto di espansione spettrale può essere verificato anche osservando che la densità di potenza
Px̃(f) è il risultato della convoluzione in frequenza
Px̃(f) = Px(f) * Ppn(f) ≃Wx⌠⌡ − WxPx(λ) Ppn(f − λ) dλ
in cui la definizione degli estremi di integrazione tiene conto del fatto che
Px(f) ≈ 0 per
|f| > Wx. Considerando ora che
Wp ≫ Wx, notiamo che per
|λ| ≤ Wx si ha
Ppn(f − λ) ≃ Ppn(f), e quindi
Px̃(f) ≈ [Wx⌠⌡ − WxPx(λ) dλ ] Ppn(f) = Px Ppn(f)
Infine, x̃(t) è usato per modulare am-bld-ps una portante a frequenza f0, producendo il segnale xm(t) = x̃(t) cos2πf0t. 16.9.2.1 Guadagno di processo
E’ il termine adottato per indicare il rapporto
tra la banda del segnale
allargato e quella del segnale di partenza. Il
processing gain varia tipicamente tra 10 e 10000 volte, ossia tra 10 e 40 dB, e come vedremo rappresenta una misura del miglioramento dell’
snr nel caso di presenza di segnali interferenti.
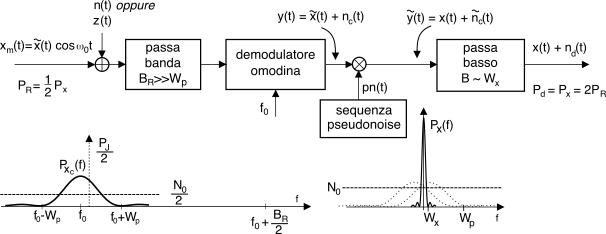
Proseguiamo l’analisi considerando lo schema di ricevitore schematizzato in fig.
16.49, nella cui parte sinistra è mostrato il segnale modulato ricevuto
xm(t) = x̃(t) cosω0t con potenza
PR = 12 Px, a cui si sovrappone un disturbo gaussiano
n(t) (od un interferente a banda stretta
z(t)). Entrambi (segnale e disturbo) attraversano quindi il filtro passabanda di ricezione, caratterizzato da una banda di rumore
BR ≫ Wp ≫ Wx in quanto deve lasciar passare l’intero spettro
allargato, compresi i suoi lobi laterali.
Dopo demodulazione omodina si ottiene il nuovo segnale di banda base
y(t) = x̃(t) + nc(t) in cui
nc(t) è la componente in fase del disturbo. A questo punto avviene l’operazione di
despreading che si avvale della possibilità per il ricevitore di generare la stessa sequenza
pn usata in trasmissione, in forma
temporalmente sincrona, in modo da poter scrivere
ỹ(t) = [x̃(t) + nc(t)]pn(t) = x(t)pn2(t) + nc(t)pn(t) = x(t) + ñc(t)
in virtù dei valori
±1 assunti da
pn(t). Pertanto, mentre il messaggio
x(t) è tornato quello precedente all’allargamento,
n(t) e/o il disturbo
z(t) subiscono le
spreading descritto al §
16.9.2. Un successivo filtraggio passa-basso con banda
Wx pari a quella di segnale produce infine il risultato
yd(t) = x(t) + nd(t), in cui il segnale utile ha potenza
Pd = Px = 2 PR, mentre per il termine di disturbo additivo
nd(t) è stata rimossa la potenza che cade al di fuori della banda di segnale.
16.9.2.3 Prestazioni in presenza di rumore
La componente in fase (dopo demodulazione omodina) del rumore bianco
n(t) con densità di potenza
Pn(f) = N0⁄2 ha densità
Pnc(f) = N0rectBR(f) (vedi §
14.1.3) e dunque
autocorrelazione
Rnc(τ) = N0BR sinc(BRτ)
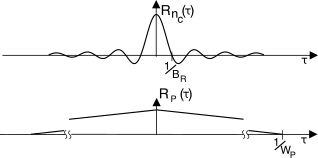
Allo scopo di valutare la densità di potenza
Pñc(f) del rumore
ñc(t) dopo despreading, con l’aiuto della figura a lato osserviamo che l’autocorrelazione di
ñc(t) è pari a
Rñc(τ) = Rnc(τ) Rp(τ), e che
Rnc(τ) ≃ 0 con
|τ| ≫ 1BR ≪ 1Wp, mentre
Rp(τ) ≃ 1 con
|τ| ≪ Tp = 1Wp: pertanto possiamo scrivere
Rñc(τ) ≃ Rnc(τ) e quindi
Pñc(f) ≃ Pnc(f) = N0rectBR(f)
La componente di rumore
nd(t) in uscita dall’ultimo passa basso con banda
≃ Wx ha pertanto una potenza
Nd ≃ 2N0Wx, permettendo di valutare il rapporto segnale-rumore dopo demodulazione come
⎛⎝PxPnc⎞⎠d = 2 PR2N0Wx = PRN0Wx
ossia proprio pari all’
SNR di sistema (pag.
1), mostrando come la concatenazione delle operazioni di spreading e despreading
non alteri le prestazioni del processo di modulazione nei confronti del rumore bianco.
16.9.2.4 Prestazioni in presenza di un tono interferente
Mostriamo che se il termine di disturbo additivo
z(t) occupa una banda relativamente stretta in rapporto a
BR, allora la sua potenza dopo demodulazione risulterà
ridotta di un fattore pari al guadagno di processo
Wp⁄Wx. Come caso limite consideriamo un
tono interferente sinusoidale z(t) (
o jammer) centrato a frequenza
f0 + fz ossia
z(t) = √2 Pj cos(ω0 + ωz)t
con potenza
Pz = Pj. Dopo demodulazione si ottiene
zc(t) = √2 Pj cosωzt e
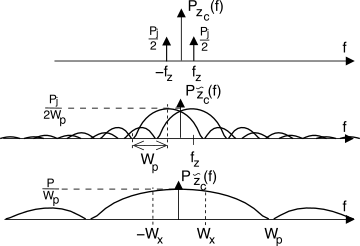
Moltiplicando quindi il tono interferente demodulato
zc(t) per
pn(t) come necessario per il despreading, si ottiene un disturbo
z̃c(t) con densità di potenza
Pz̃c(f) = Pzc(f) * Pp(f), mostrata alla riga centrale di fig.
16.51, permettendo di apprezzare l’effetto di
allargamento subito dal tono interferente. Notiamo ora che la massima interferenza si ottiene quando
|fz| ≪ Wp, al limite pari a zero, come mostrato all’ultima riga
della figura in scala espansa per il caso limite di
fz = 0. Pertanto il limite superiore della potenza interferente uscente dal passa basso con banda
Wx è
Pzd = Wx⌠⌡ − WxPz̃c(f) df ≤ 2Wx PjWp
e dunque il rapporto segnale-interferente diviene
⎛⎝PxPzd⎞⎠d ≥ 2 PR Wp2WxPj = PRPj WpWx
che rappresenta un miglioramento esattamente pari al guadagno di processo
Gp, eq.
(21.73).
16.9.2.5 Accesso multiplo CDMA
Una frequente applicazione della tecnica spread spectrum è quella di permettere la comunicazione
contemporanea di una pluralità di soggetti, possibile qualora ognuno di essi adotti una diversa sequenza
pn: tale approccio prende il nome di
cdma (
Code Division Multiple Access). Mostriamo ora che con questo approccio ogni comunicazione subisce (a causa delle altre) solo un modesto innalzamento del rumore di fondo, tanto più piccolo quanto minore è il valore della
intercorrelazione tra i codici
pn utilizzati. Indichiamo con
z(t) il termine interferente (dopo demodulazione) dovuto alla presenza di
N diversi utenti, ognuno con un diverso codice
pni(t) e segnale dati
xi(t), che può essere scritto come
z(t) = N⎲⎳i = 1Ai xi(t − τi) pni(t − τi) cosθi
in cui
Ai,
τi e
cosθi sono rispettivamente ampiezza, ritardo di simbolo e fase della portante relativi all’
i-esimo utente. Assumendo ora eguali tra loro le ampiezze del segnale utile
x(t) e degli interferenti, dopo il despreading otteniamo
ỹ(t) = x(t) + [N⎲⎳i = 1xi(t − τi) pni(t − τi) cosθi ] pn(t)
Se realizziamo ora il filtro passa basso di fig.
16.49 come un integratore esteso ad un periodo di bit, ovvero un filtro adattato al segnale
nrz, il valore della sua uscita campionata al termine della durata del
k-esimo periodo di bit risulta
d(kTb) = Tbx(kTb) + N⎲⎳i = 1[ cosθikTb⌠⌡(k − 1)Tbxi(t − τi) pni(t − τi) pn(t) dt ] = Tb x(kTb) + zd(kTb)
in cui
zd(kTb) rappresenta il termine di interferenza complessiva da parte di tutti gli altri
N utenti, indicata come
interferenza multiutente o
mui (multi-user interference). Dato che i valori di
xi possono essere
±1, l’integrale calcola in effetti
l’intercorrelazione Rp0pi(τi) (§
7.1.4) tra la sequenza
pn usata per la propria trasmissione e le sequenze
pn usate dagli altri, calcolata per un ritardo
τi. Pertanto, scegliendo la famiglia di sequenze pseudo-noise in modo che esibiscano una intercorrelazione molto ridotta (in teoria nulla, se le
pn fossero esattamente
ortogonali), l’effetto degli interferenti si riduce in egual misura.
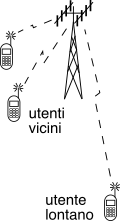
Qualora un utente di un sistema
cdma sia sensibilmente più lontano dal ricevitore rispetto agli altri, se tutti trasmettono con la stessa potenza l’attenuazione subìta dal segnale dell’utente lontano fa si che il termine
mui aumenti di importanza, anche in presenza di intercorrelazione bassa, causando un importante degrado della qualità della trasmissione. Questo fenomeno è indicato come
effetto near-far. Per ovviare al problema un sistema
cdma viene usualmente corredato di un meccanismo di
controllo di potenza, espletato dalla stazione radio base, che misurando la potenza ricevuta da ciascun utente, ne richiede la diminuzione ai vicini e/o l’aumento ai lontani, in modo da ricevere la medesima potenza da ciascuno di essi.
Prestazioni multi-utente con PN incorrelate
Consideriamo il caso in cui le trasmissioni
cdma di
K diversi utenti siano tutte ricevute con la medesima potenza
Px, e le sequenze
pn utilizzate da ciascuno di essi abbiano una intercorrelazione nulla. Allora, per una generica trasmissione la potenza interferente
Pnd risulta ridotta rispetto a quella effettivamente ricevuta di una quantità pari al guadagno di processo, e quindi il
rapporto segnale-interferenza (indicato come
sir) risulta circa pari a
SIR = PxPnd = Px(K − 1) Px⁄Gp = GpK − 1
Dato che le
pn effettivamente utilizzate
non presentano intercorrelazione nulla, il risultato mostrato costituisce una approssimazione limite rispetto alla quale valutare la qualità delle prestazioni effettivamente ottenute. Nel caso di trasmissione a due livelli la prob. di errore
(21.40) minima (a causa degli interferenti) diviene quindi
PBPSKe(bit) = 12 erfc{√SIR} = 12 erfc⎧⎨⎩√GpK − 1⎫⎬⎭
Infine, per tener conto allo stesso tempo sia dell’effetto degli interferenti che del rumore gaussiano comunque presente, può essere usato il
rapporto segnale-rumore più interferente (o
sinr) definito come
SINR = PxPnd + Pn = ⎛⎝Pnd + PnPx⎞⎠− 1 = ⎛⎝K − 1G + N0Eb⎞⎠− 1
ossia pari
al parallelo degli
snr, come discusso a pag.
1.
Esempio In un sistema cdma-dsss si desidera una Pe = 10 − 6, a cui la tecnica di modulazione adottata fa corrispondere un Eb⁄N0 = 13 dB. Trascurando il rumore termico, determinare il massimo numero K di utenti contemporaneamente attivi se Gp = 30 dB.
16.9.3 Sequenze pseudo casuali
Accenniamo brevemente ad alcune tipologie di sequenze pseudo noise.
Sequenze di massima lunghezza
Una prima possibilità è quella delle sequenze-
m, o
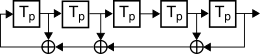
di massima lunghezza, ottenute mediante dei registri a scorrimento controreazionati con
m ritardi,
simili a quelli discussi a proposito del
crc (pag.
1) ma con la struttura mostrata in figura, in cui non è presente nessun ingresso esterno ed il bit che
rientra è calcolato in base all’
or esclusivo di una combinazione di bit di stato. Dato che con
m bit si ottengono
2m configurazioni dello stato, ma che quella
tutti zeri arresterebbe il processo di generazione, le sequenze di
massima lunghezza sono composte da
L = 2m − 1 bit (ognuno dei quali corrisponde ad una diversa configurazione dello stato) che si ripetono ciclicamente, e sono ottenute per particolari scelte di quali bit far partecipare alla controreazione.
Tra le proprietà positive di questa famiglia annotiamo la
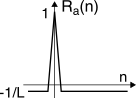
quasi equiprobabilità dei bit uno e zero, la equa distribuzione delle sequenze di bit uguali, ed una
autocorrelazione ciclica Ra(n) = 1L ∑L− 1k = 0 aka(k + n) mod L
che vale 1 per
n = 0 ed
− 1⁄L altrimenti (vedi figura). D’altra parte, l’
intercorrelazione ciclica tra due diverse sequenze-
m (di uguale lunghezza
L) presenta valori massimi che sono una percentuale apprezzabile di
Ra(0), rendendo necessario individuare altre soluzioni per i casi di accesso multiplo.
Sequenze di Gold e Kasami
Le sequenze di Gold si ottengono eseguendo l’or esclusivo bit a bit di due diverse sequenze-m a e b di uguale lunghezza L; ripetendo il procedimento per tutti i 2m − 1 possibili scorrimenti temporali di b rispetto ad a, ed includendo a, si ottengono 2m diverse sequenze, con una intercorrelazione massima pari a √2⁄L. Una soluzione lievemente diversa è quella di Kasami, in cui una delle due sequenze-m di partenza viene decimata ciclicamente, e che produce 2m⁄2 sequenze, con intercorrelazione massima pari a 1 √L.
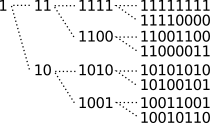
Sequenze di Walsh-Hadamard
Si tratta di sequenze ortogonali, ovvero per le quali risulta ∑L− 1k = 0 akbk = 0, ossia a e b sono sequenze incorrelate qualora allineate, e che sono generate mediante l’algoritmo iterativo schematizzato alla figura che segue, che individua un numero di L = 2m sequenze, di lunghezza L.
Possono dunque essere usate nel contesto di un sistema di accesso multiplo qualora gli apparati possano essere sincronizzati tra loro, come per il collegamento
in discesa tra una stazione radio base ed i terminali radiomobili associati ad essa. Il lato meno positivo di queste sequenze è una autocorrelazione che presenta diversi picchi secondari, e dunque non sono idonee ad assolvere la funzione di sincronizzazione (§
16.11.1). D’altra parte, la proprietà di ortogonalità può altresì essere sfruttata per realizzare una
segnalazione ortogonale (§
7.6.2) nel contesto di una comunicazione punto-punto.
Presentano valori di autocorrelazione (
non ciclica)
Ra(n) = 1L ∑L − 1 − |n|m = 0 ambm + |n| con valori Ra(0) = 1 e |Ra(n)| ≤ 1⁄L per 1 ≤ n < L, e come le sequenze-m esibiscono buone proprietà rispetto al bilanciamento ed alle corse. L’aspetto negativo è che la massima lunghezza di sequenza conosciuta è L = 13, e con questa lunghezza, ne esiste solo una! Nonostante ciò, sono utilizzate ad esempio nei sistemi di accesso WiFi.
16.9.4 Frequency Hopping
Si tratta di una diversa tecnica
spread spectrum, in cui la sequenza
pn è di tipo
multilivello, ed è utilizzata in uno schema
l-fsk incoerente (§
16.5) per cambiare in continuazione la frequenza portante a cui avviene la trasmissione, tipicamente
fsk anch’essa (vedi figura
16.56), da cui il nome di
saltando di frequenza (traduzione letterale di
Frequency Hopping). Per una corretta ricezione, è necessaria una accurata sincronizzazione temporale tra la
pn usata in trasmissione e quella in ricezione.
Anche in questo caso si verifica un fenomeno di espansione spettrale, ma stavolta non tutta la banda è occupata in modo
permanente come nel
dsss, ma anzi durante ogni
salto si occupa solo la banda necessaria alla modulazione
non allargata. In questo caso un disturbo a banda stretta provoca interferenza solo durante il salto che occupa la sua stessa frequenza, e dunque può essere facilmente contrastata adottando una codifica di canale (§
17.4). Inoltre, la tecnica
fhss è proficuamente impiegata in sistemi di accesso multiplo
cdma, dato che possono avvenire contemporaneamente più trasmissioni
fhss utilizzando per esse differenti sequenze
pn a bassa intercorrelazione.
Se il periodo di chip (ovvero il tempo per cui il vco permane sulla stessa frequenza) è più breve del periodo di simbolo, il sistema è detto fast frequency hopping o ffhss, mentre se è maggiore è detto slow fh o sfhss.
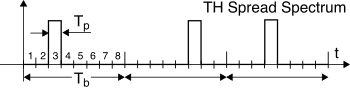
16.9.5 Time Hopping o UWB
In questo caso la trasmissione avviene su intervalli temporali molto ridotti, e dunque con una occupazione di banda molto elevata (a volte indicata come
ultra wide band o
uwb); l’altro aspetto in comune con le tecniche a spettro espanso è il posizionamento
pseudo-casuale degli impulsi nell’ambito di una trama temporale, in base ad una sequenza
pn. La figura a lato mostra un segnale
thss di banda base, in cui per ogni bit viene trasmesso un chip con
Tp ≪ Tb, posizionato su (ad es.) una di otto possibili posizioni, in maniera pseudo casuale.