16.12.1 Ortogonalità tra simboli sinusoidali
Al §
16.5.1 si è introdotta la modulazione
fsk ortogonale, e nelle note è iniziata la discussione relativa alla condizione di ortogonalità tra la forma d’onda sinusoidale di durata
Ts ricevuta, e quella prodotta al ricevitore come ingresso ai correlatori di un banco. Prendiamo pertanto ora in considerazione segnali del tipo
sk(t) = cos [2π(f0 + k ⋅ Δ)t + φk] con k intero
separati da un intervallo di frequenza
Δ, in cui è inclusa una differenza (o errore) di fase aleatorio
φk tra le forme d’onda, in modo da esaminare le differenze tra il caso di modulazione coerente ed incoerente, ovvero con
φk = 0 ∀k, oppure
φk v.a. incorrelate uniformi tra
0 e
2π.
Iniziamo dunque con lo sviluppare l’espressione dell’integrale di intercorrelazione tra due di questi segnali
ρ = Ts⌠⌡0sn(t)sm(t)dt = Ts⌠⌡0cos [2π(f0 + mΔ)t] cos[2π(f0 + nΔ)t + φ] dt
che quando si annulla indica la condizione di ortogonalità. Facendo uso della relazione
cosα cosβ = 12 [cos(α + β) + cos(α − β)] e riferendoci per semplicità al caso di due frequenze contigue (ponendo
m = 0 ed
n = 1) si ottiene
Verifichiamo che il primo integrale della somma assume un valore nullo indipendentemente da
φ quando
2f0 + Δ = kTs, poiché in tal caso in un intervallo
Ts entrano un numero intero
k di periodi, ed il coseno ha valor medio nullo. Concentriamoci allora sul valore di
Δ che annulla anche il secondo integrale, che riscriviamo facendo uso della relazione
cos(α − β) = cosα cosβ + sinα sinβ:
Osserviamo ora che qualora
φ = 0 (coerenza di fase) il secondo termine della
(21.76) si annulla per qualunque
Δ. Se a questo punto esaminiamo solamente il primo termine, individuiamo le condizione di ortogonalità sul valore di
Δ per il caso di
Quando
φ = 0 il termine
sin(2πΔTs)2πΔTs = sinc(2ΔTs) della
(21.76) si annulla per
Δ = k2Ts, e quindi la
minima spaziatura tra portanti risulta
Δ = 12Ts = fs2; pertanto, le frequenze utilizzate dovranno essere del tipo
f0 + kfs2.
Per fare in modo che
anche il primo termine della (
21.75) si annulli deve sussistere la relazione già osservata
2f0 + Δ = kTs = kfs, sostituendo nella quale il vincolo
Δ = fs2 appena trovato fornisce
2f0 + Δ = 2f0 + fs2 = kfs
a cui corrisponde la la condizione
f0 = fs2k − 14
ossia
f0 deve essere scelta come uno tra i valori
14fs, 34fs, 54fs, 74fs, …, il che significa che la portante di riferimento
f0 da cui partire deve essere essa stessa ortogonale alle frequenze che codificano i simboli: infatti in tal modo ogni termine della serie dista dall’altro per una frequenza pari a
fs2, coincidente con il valore
Δ necessario a che le frequenze di segnalazione siano ortogonali.
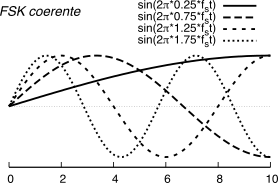
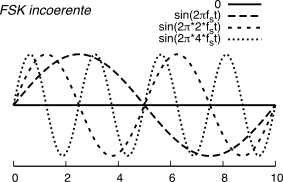
La parte sinistra della figura
16.66 quindi rappresenta, disegnate in un intervallo pari a
Ts, sia le portanti
f0 che possono essere usate, sia le prime frequenze
fk = k ⋅ Δ che è possibile adottare per un modulazione
fsk coerente basata sul valore minimo di
f0 pari a
14fs.
Nel caso in cui
f0 non assuma uno dei valori individuati il primo termine di (
21.75) non si annulla, ma se
f0 ≫ 1Ts, risulta trascurabile rispetto al secondo. Pertanto, se
f0 ≫ fs la scelta di
f0 non è più determinante.
In questo caso si ha
φ ≠ 0. In generale la (
21.76) presenta entrambi i termini; mentre il primo (come già osservato) si annulla per
Δ = k2Ts, il secondo invece è nullo solo se
Δ = kTs. Questa circostanza determina il risultato che quando
φ ≠ 0 i segnali
sk(t) sono ortogonali purché la spaziatura tra portati sia
doppia della precedente, e pari cioè a
Δ = fs.
Torniamo ad esaminare la (
21.75): ora il suo primo termine si annulla se
2f0 + Δ = 2f0 + fs = kfs, che determina la condizione
f0 = fsk − 12
ossia
f0 = 0, 12fs, fs, 32fs, …. Notiamo come la spaziatura
fs2 tra i possibili valori per la portante di riferimento
f0 sia identica al caso precedente, mentre la spaziatura necessaria alle frequenze di segnalazione
fk = k ⋅ Δ è raddoppiata. La circostanza che ora sia ammessa anche una “portante a frequenza nulla” consente quindi di tracciare la parte destra della figura
16.66, che mostra le prime frequenze di segnalazione che è possibile adottare per una modulazione
fsk incoerente basata sul valore minimo di
f0 = 0.
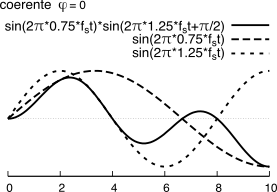
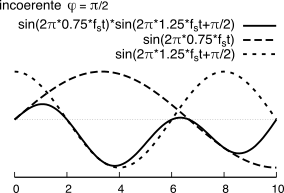
In figura
16.67 è mostrato il risultato del prodotto di due frequenze distanti
fs2 e calcolate in assenza di errore di fase (a sinistra) e con un errore di fase pari a
φ = π2. Si può notare come in questo secondo caso si perda l’ortogonalità tra i segnali, essendo il risultato prevalentemente negativo.
16.12.2 Prestazioni della modulazione OFDM
Il calcolo della
Pe per bit accennato al §
16.8.5 si basa su quello relativo alle probabilità di errore
Pen condizionato alle singole portanti. Dato che la portante
n-esima trasporta
Mn bit/simbolo, la probabilità che un bit generico provenga dalla portante
n-esima risulta pari a
Pr(n) = MnM e quindi la probabilità che sia errato è pari a
16.12.2.1 Calcolo della Pe per portante
Per determinare il valore di
Pen per la portante n-esima si applica il risultato trovato al §
16.3.1 per la modulazione
qam, che esprime
Pen in funzione del numero di livelli
Ln = 2Mn e del rapporto
⎛⎝EbN0⎞⎠n per tale frequenza. Ma l’eq.
(21.47) è ricavata considerando la densità di potenza del rumore in ingresso al ricevitore limitata da un filtro con banda pari a quella del segnale
qam, mentre ora tale filtro lascia passare l’intera banda
NΔ occupata dal segnale
ofdm, e quindi occorre valutare l’effetto prodotto da questo rumore sui valori
an ottenuti mediante
fft. Inoltre, vorremmo pervenire ad un risultato valido anche in presenza di rumore non bianco, e/o di una distribuzione di potenza sulle portanti non uniforme. Pertanto, al posto del rapporto
Eb⁄N0 che compare nella
(21.47) utilizziamo ora il rapporto
SNRn tra la quota di potenza di segnale che raggiunge l’
n-esimo decisore, e la varianza (dovuta al rumore) della v.a.
an su cui si basa tale decisione, ottenendo così
ed in cui
Pαn esprime la probabilità di errore su di uno dei rami (in fase od in quadratura) della n-esima costellazione qam con Ln punti, che rappresentano gruppi di bit secondo la codifica di Gray. Per il calcolo di
SNRn = PcRnPcNn = PsRnPsNn = 12 PRn12 PNn = PRnPNn
osserviamo che la potenza PRn dell’inviluppo complesso del segnale ricevuto sulla portante n-esima è pari a
PRn = 2 PRn = 2 T0T αn P
in cui P è la potenza totale ricevuta, e αn = PnP è la frazione di potenza assegnata alla n-esima portante. Resta quindi da determinare PNn. 16.12.2.2 Potenza di rumore per portante
Per quanto riguarda
PNn, si tratta di applicare la (
21.65) alla sequenza
{( − 1)hn(hTc)} dei campioni dell’inviluppo complesso del rumore, e determinare il valore
PNn = E{(Nn)2} = σ2Nn in cui Nn = 1N N− 1⎲⎳h = 0( − 1)hn(hTc)e −j2πhNn
tenendo conto del fatto che i valori
n(hTc) sono a media nulla, che (con
n fissato) la
fft ne effettua una combinazione lineare con coefficienti
e −j2πhNn, e che essendo
n(t) ergodico è possibile scambiare medie temporali e di insieme. Sviluppando
(Nn)2 = NnN * n = 1N2 N− 1⎲⎳h = 0 N− 1⎲⎳k = 0( − 1)h − kn(hTc)n*(kTc)e −j2πh − kNn
e tenendo conto che
E{( − 1)h − kn(hTc)n*(kTc)} = e jπ(h − k)RN((h − k)Tc)
otteniamo
in cui l’ultima riga semplifica l’espressione introducendo la sequenza
{z(m)} di lunghezza
N, che si ottiene campionando
agli istanti
t = mTc con
Tc = 1NΔ. Mostriamo ora come, per
N sufficientemente elevato, la (
21.79) possa essere calcolata in funzione dei campioni di
Z(f) = F {z(t)}, ed in particolare di come risulti
PNn ≃ Δ ⋅ Z(f)|f = nΔ ≃ 4Δ ⋅ PN(fn)
Analizzando i termini che compaiono in (
21.80), osserviamo che il prodotto
RN(t)e j2πt2Tc ha trasformata pari a
PN(f), traslata in frequenza di
− 12Tc = − NΔ2, ovvero
F {RN(t) e j2πt2Tc} = PN⎛⎝f − NΔ2⎞⎠
mentre il termine
⎛⎝1 − |t|NTc⎞⎠ = tri2NTc(t) = tri2Δ(t) possiede come noto trasformata
F { tri2Δ(t)} = 1Δ sinc2⎛⎝fΔ⎞⎠; pertanto per
N elevato il prodotto
z(t) = RN(t)e j2πt2Tc ⋅ tri2Δ(t) ha trasformata
Z(f) = PN⎛⎝f − NΔ2⎞⎠ * 1Δ sinc2⎛⎝fΔ⎞⎠ ≃ PN⎛⎝f − NΔ2⎞⎠
avendo approssimato
1Δ sinc2⎛⎝fΔ⎞⎠ come un impulso di area unitaria, per
NΔ grande rispetto a
Δ.
Dato che
PN(f) è limitato in banda tra
± NΔ2, allora
Z(f) è limitato in una banda compresa tra
f = 0 ed
f = NΔ, e
z(t) è perfettamente rappresentato dai suoi campioni
z(m) = z(mTc) che compaiono nella (
21.79); in particolare, per
N sufficientemente elevato si ottiene che
PNn = 1N N− 1⎲⎳m = − (N − 1)z(m)e −j2πmNn ≃ Δ ⋅ Z(f)|f = nΔ = = Δ ⋅ PN⎛⎝nΔ − NΔ2⎞⎠ = Δ ⋅ PN⎛⎝Δ⎛⎝n − N2⎞⎠⎞⎠ = = 4Δ ⋅ P + N⎛⎝f0 + Δ⎛⎝n − N2⎞⎠⎞⎠ = 4Δ ⋅ PN(fn) = 2Δ ⋅ N0(fn)
(passaggi alla nota) in cui si è tenuto conto che PN(f) = 4 P+N(f + f0) e si è indicata la densità di potenza in ingresso come PN(f) = N0(f)2.
16.12.2.3 Prestazioni per portante
Siamo finalmente in grado di scrivere
SNRn = PRnPNn = 2 T0T αn P2Δ N0(fn) = T0T αnT0 PN0(fn) = T0T αnEsN0(fn) = = T0T αn EbMN0(fn) = T0T EbnEb EbMN0(fn) = T0T EbnMN0(fn)
avendo posto
T0 P = Es = EbM pari all’energia di un simbolo di durata
T0 = 1Δ, ed avendo riscritto
αn = PnP come
αn = EbnEb in modo da porre in evidenza la
Ebn della portante n-esima. La
Pe per portante risulta quindi
16.12.2.4 Caso di rumore bianco
Se
PN(f) non dipende da
f, possiamo scrivere
P + N(f) = N02 rectNΔ(f − f0)
e semplificare la (
21.81) sostituendo ad
N0(fn) la costante
N0. In questo caso il risultato
PNn = 2Δ ⋅ N0 può essere ottenuto direttamente dalla (
21.79): risulta infatti
RN(t) = F −1{ PN(f)} = F −1{4 P+N(f + f0)} = 2 N0 NΔ sinc(NΔt)
e dunque
RN(t) = 0 con
t = mTc = mNΔ per
m ≠ 0. Ciò in definitiva permette di scrivere
PNn = 1NRN(0) = 1N 2 N0 NΔ = 2Δ ⋅ N0
16.12.2.5 Confronto con la portante singola
Proviamo a verificare se la modulazione ofdm è vantaggiosa in termini di prestazioni rispetto ad una qam monoportante che trasporti il medesimo flusso binario fb, occupi la stessa banda, ed a parità di potenza impiegata.
Nel caso
ofdm, considerando un tempo di guardia
Tg = T − T0 nullo, in presenza di rumore bianco, e scegliendo un intervallo di simbolo
T0 = 1Δ da cui derivare
MOFDM = T0 ⋅ fb, si ottiene
αn = 1Ñ e dunque valori
Ebn = αnEb = EbÑ uguali per le diverse portanti; pertanto la
21.81 diviene
POFDMe = Pe ⁄ n = 2ÑMOFDM ⎛⎝1 − 1√Ln⎞⎠ erfc⎧⎨⎩√32 EbN0 1Ñ MOFDMLn − 1⎫⎬⎭
Nel caso
qam a portante singola, considerando un impulso a coseno rialzato e roll-off
γ = NÑ − 1 si determina una occupazione di banda pari a
B = fs(1 + γ) che, se eguagliata a quella del caso
ofdm, fornisce
fs = ÑΔ = ÑT0 e quindi
MQAM = fbfs = MOFDMÑ. Pertanto, visto il risultato del §
16.3.1 si ottiene
PQAMe = 2MQAM ⎛⎝1 − 1√L⎞⎠ erfc⎧⎨⎩√32 EbN0 MQAML − 1⎫⎬⎭ = 2ÑMOFDM⎛⎝1 − 1√L⎞⎠ erfc⎧⎨⎩√32 EbN0 1Ñ MOFDML − 1⎫⎬⎭
che risulta identico a
POFDMe qualora si noti che
Ln = 2Mn = 2MOFDMÑ e
L = 2MQAM = 2MOFDMÑ = Ln.
16.12.3 Allocazione ottima della potenza OFDM
Affrontiamo la derivazione della
(21.69) fornita a pag,
1 come soluzione al problema di trovare la
PR(f) che rende massima la quantità
con
If = {f: PR(f) > 0}, nel rispetto dei vincoli
⌠⌡f ∈ IfPR(f)df − PR = 0 e PR(f) ≥ 0
che esprimono rispettivamente la limitazione sulla potenza totale
PR a disposizione e la necessità che la densità di potenza
PR(f) del segnale
ofdm non sia negativa. Un problema di massimo vincolato siffatto viene tipicamente affrontato con la tecnica dei
moltiplicatori di Lagrange (vedi
9.6.1) tranne che ora la presenza del vincolo di tipo disuguaglianza
PR(f) ≥ 0 comporta alcune considerazioni aggiuntive, note come
condizioni di Karush–Kuhn–Tucker, i cui aspetti però non approfondiamo.
Scriviamo dunque la funzione
lagrangiana (10.258) come
L(PR(f), λ) = ⌠⌡ ln ⎛⎜⎝1 + PR(f)PN(f)⎞⎟⎠ df + λ(⌠⌡PR(f)df − PR) = ⌠⌡ ⎡⎣ln ⎛⎝1 + PR(f)PN(f)⎞⎠ + λPR(f)⎤⎦ df − λPR
in cui si sono usati i logaritmi naturali anziché in base 2 dato che ciò comporta solamente una variazione di ampiezza e non inficia il procedimento di massimizzazione. Valutiamo quindi la derivata parziale
in cui come al §
9.6.2 ci si è avvalsi della proprietà di
derivata sotto il segno di integrale. Il massimo della capacità
C (eq.
(21.82)) si ottiene eguagliando
(21.83) a zero, ovvero azzerando il termine tra parentesi quadre; per questa via otteniamo
PR(f) = − 1λ − PN(f)
ma, per rispettare i vincoli, scegliamo un valore
μ = − 1λ > 0 tale che scrivendo
si abbia sempre
PR(f) ≥ 0 e risulti
∫ PR(f)df = PR. A questo punto è immediato riconoscere la
(21.84) come una notazione alternativa delle
(21.69) di pag.
1.