2.1 Prerequisiti trigonometrici
Dato che come vedremo un segnale periodico può essere espresso come una combinazione di funzioni trigonometriche, intraprendiamo i passi necessari a poterle descrivere nei termini di funzioni esponenziali complesse, che a loro volta intervengono in modo massiccio nella rappresentazione frequenziale di Fourier.
2.1.1 Numeri complessi
Un numero complesso
x è costituito da una coppia di valori
a e
b entrambi
reali che ne costituiscono la parte reale
a e quella immaginaria
b, e viene scritto come
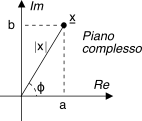
detta rappresentazione in
coordinate cartesiane o rettangolari, che lo mette in corrispondenza con un punto in un
piano complesso. Le operazioni di somma e prodotto tra due numeri complessi
x = a + jb e
y = c + jd danno come risultato
x + y = (a + c) + j(b + d) e x ⋅ y = (ac − bd) + j(ad + bc)
mentre l’inverso di un numero complesso risulta
1x = 1a + jb = a − jb(a + jb)(a − jb) = aa2 + b2 − jba2 + b2
Il numero complesso
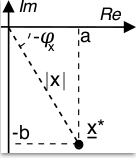
x* = a − jb prende il nome di
coniugato di
x, per il quale valgono le relazioni
x + x* = 2a = 2ℜ{x} e
x − x* = 2jb = 2jℑ{x}.
Ricorrendo alle relazioni trigonometriche
a = |x|cosφx e
b = |x|sinφx un numero complesso
x può essere anche espresso in
coordinate polari come
in cui
|x| = √a2 + b2 prende il nome di
modulo di
x e
φx = arg{x} = arctan ba prende il nome di
fase o
argomento. Risulta quindi evidente che
|x|2 = a2 + b2 = x ⋅ x*, mentre
1x = x*|x|2. Infine, In virtù della periodicità di
sin e
cos, due numeri complessi con uguale modulo ma fase che differisce per multipli di
2π sono
indistinguibili. 2.1.2 Formula di Eulero
Si può mostrare che qualora la serie di potenze in cui può essere sviluppata la funzione esponenziale
ez (pag.
1) sia valutata per un argomento
z = jb completamente immaginario, essa eguaglia la somma delle serie di potenze in cui è possibile sviluppare
la funzione
cosb + jsinb. Questo risultato prende il nome di
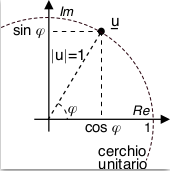
formula di Eulero, e mostra come l’esponenziale immaginario
e±jφ sia un particolare numero complesso con modulo pari ad uno e fase
φ espresso come
La relazione
(10.3) consente di scrivere le funzioni trigonometriche in termini di esponenziali complessi come
cos φ = e jφ + e −jφ2 e sin φ = e jφ − e −jφ2j
Tali relazioni possono tornare utili nel semplificare i calcoli, trasformando i prodotti tra funzioni trigonometriche in somme di angoli . Ma sopratutto, la rappresentazione di un numero complesso
x in coordinate polari
(10.2) può essere riscritta in base alla
(10.3) come
detta anche
rappresentazione esponenziale di
x.
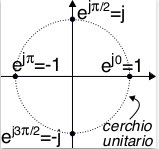
In tal modo i numeri complessi di modulo unitario e che presentano la sola parte reale o che sono puramente immaginari possono essere rappresentati come in figura a lato, mentre il coniugato x* di un numero complesso x viene ridefinito come quel numero complesso con uguale modulo e fase cambiata di segno, ovvero x* = a − jb = |x|e −jφ.
Infine, il prodotto tra due numeri complessi
x ed
y può essere agevolmente calcolato come
|x|e jφx ⋅ |y|e jφy = |x||y| ⋅ e j(φx + φy) = |z|e jφz in cui |z| = |x||y| e φz = φx + φy
o, detto in altri termini
il modulo del prodotto tra numeri complessi è pari al prodotto tra i moduli, e la fase pari alla somma delle fasi
e dunque, come corollario, per il rapporto si ottiene xy = |x||y| e j(φx − φy) .
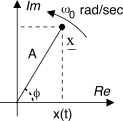
Un segnale del tipo
x(t) = Acos(2πf0t + φ) è completamente rappresentato dal numero complesso
x = Ae jφ detto
fasore, la cui conoscenza permette di riottenere il segnale
originario mediante la relazione
x(t) = ℜ{x ⋅ e j2πf0t}, che una volta sviluppata risulta infatti pari a
x(t) = ℜ{Ae jφ ⋅ e j2πf0t} = A ⋅ ℜ{e j(2πf0t + φ)} = = A ⋅ ℜ{cos(2πf0t + φ) + jsin(2πf0t + φ)} = = Acos(2πf0t + φ)
Osserviamo che il risultato è interpretabile graficamente come aver impresso al fasore
x una rotazione di velocità angolare ω0 = 2πf0 radianti/secondo in senso antiorario, ed aver proiettato il risultato sull’asse reale.
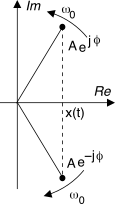
In alternativa, possiamo esprimere il segnale
x(t) di partenza anche come
coinvolgendo in tal modo anche le
frequenze negative, cioè tenendo conto di un secondo vettore contro-rotante, coniugato al primo rotore e che si muove in senso
orario, che quindi ha una parte immaginaria di segno sempre opposto al primo, e che è moltiplicato per il coniugato del fasore. Vedremo tra breve che la
(10.5) coincide con l’espressione della
serie di Fourier per il caso in questione.