6.4 Trasformazione di v.a. e cambio di variabili
Quando più v.a. si combinano con leggi diverse dalla somma, il risultato del §
6.2.5 non è più sufficiente a fornire una espressione per la d.d.p. risultante. Illustriamo quindi il procedimento analitico generale, necessario ad ottenere una espressione per la d.d.p. di una generica funzione di v.a.
6.4.1 Caso unidimensionale
Consideriamo una prima v.a.
X, ed una seconda
Y da essa derivata per mezzo della relazione
y = f(x), che si applica alle determinazioni
x di
X. Nel caso in cui
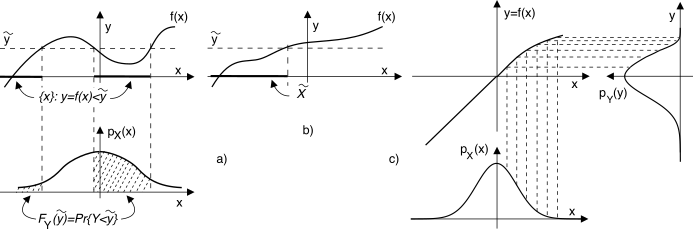
f(x) sia monotona non decrescente (vedi fig.
6.13-a), e indicando con
x = g(y) la corrispettiva funzione inversa, la caratterizzazione probabilistica di
Y nei termini della sua d.d.p.
pY(y) può essere ottenuta a partire da quella di
X nei termini della funzione di distribuzione di
Y, come
e calcolando poi
pY(y) = dFY(y) dy .
D’altra parte, qualora la trasformazione
f(x) non sia monotona come nel caso mostrato in fig.
6.13-b), la
(10.131) non è più usabile, in quanto i valori
y ≤ ỹ hanno origine da due diversi intervalli di
X, in corrispondenza dei quali l’area sottesa dalla
pX(x) individua la probabilità cercata.
Procedendo con ordine, trattiamo prima il caso di
f(x) monotona crescente come in fig.
6.13-a), in cui per ogni valore di
ỹ esiste un solo intervallo di
X̃ ⊂ X tale che
y = f(x)|x ∈ X̃ ≤ ỹ, e la (
10.131) può essere riscritta come
FY(y) = Pr{X ≤ g(y)} = FX(x = g(y))
che, derivata, permette di giungere alla espressione che consente il calcolo della
pY(y):
La (
10.132) indica che la nuova v.a.
y = f(x) possiede una d.d.p. pari a quella di
x, calcolata con argomento pari alla funzione inversa
x = g(y), moltiplicata per la derivata di
g(y). La d.d.p. della v.a. risultante si presta anche ad un processo di costruzione grafica, come esemplificato in fig.
6.13-c).
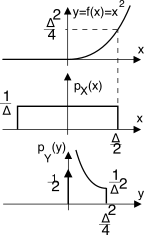
Esempio Determinare
pY(y), qualora risulti
y = f(x) = ⎧⎨⎩ 0 con x ≤ 0 x2 con x > 0 , nel caso in cui
pX(x) = 1 Δ rectΔ(x).
Osserviamo innanzitutto che tutte le determinazioni
x ≤ 0 danno luogo ad un unico valore
y = 0; pertanto si ottiene
pY(0) = 12 δ(y). Per
0 < y ≤ Δ2 4 (corrispondente ad
0 < x ≤ Δ 2 ) si applica la teoria svolta, ottenendo
FY(y) = Pr{x ≤ √y} = FX(√y), e dunque
pY(y) = dFY(y)dy = dFX(x)dx||x = √y d(x = √y)dy = 1 Δ 1 2√y
in cui l’ultima eguaglianza tiene conto che
dFX(x) dx = pX(x), che vale
1Δ per tutti gli
x nell’intervallo in considerazione. L’ultima curva mostra la d.d.p risultante per questo esempio.
Se invece la
f(x) è monotona
ma decrescente, consideriamo semplicemente che le probabilità
Pr{x ≤ X ≤ x + dx} = pX(x)dx e
Pr{y ≤ Y ≤ y + dy}|y = f(x) = pY(y)dy devono essere uguali, ma dato che con
f(x) decrescente ad un
dx positivo corrisponde un
dy negativo, prendiamo il valore assoluto di entrambi:
pX(x)|dx| = pY(y)|dy|; sostituendo quindi
x con la sua funzione inversa
x = g(y) e ri-arrangiando si ottiene
che è la versione più generale del risultato
(10.132).
Esempio Qualora
f(x) sia una relazione lineare
y = ax + b possiamo scrivere
x = g(y) = y − ba e
ddy g(y) = 1 a ; pertanto la
(10.133) si traduce in
pY(y) = 1|a|pX⎛⎝y − b a ⎞⎠, ovvero la nuova v.a.
Y possiede una d.d.p. con lo stesso andamento di
pX(x), ma traslata di
b e compressa o espansa di
a.
Trasformazione non monotona
In questa circostanza due o più valori di
X producono lo stesso valore di
Y (vedi fig.
6.13-b)), e non esiste una funzione inversa
x = g(y) univoca. In tal caso si suddivide la variabilità di
X in più intervalli
i, in modo che per ciascuno di essi possa definirsi una
fi(x) monotona: tali intervalli individuano eventi mutuamente esclusivi, e dunque si può calcolare il lato destro di
(10.133) per ogni funzione inversa
gi(y) = f− 1i(x), e quindi sommare i risultati per ottenere
pY(y).
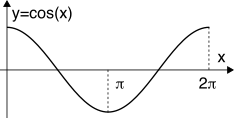
Esempio Consideriamo la funzione
y = f(x) = cos(x) in cui
x è una v.a. con d.d.p. uniforme
pX(x) = 12π rect2π(x − π).
Dato che per
0 ≤ x ≤ π il coseno è decrescente, mentre per
π ≤ x ≤ 2π è crescente, applichiamo la
(10.133) su questi due intervalli. Per il primo si ha
x = g1(y) = arccos(y), la cui derivata vale
dg1(y)dy = − 1 √1 − y2 , mentre
pX(x) è costante e pari a
12π indipendentemente da
x, dunque
pX(g1(y)) = 1 2π . Per il secondo intervallo la funzione inversa vale ancora
x = g2(y) = arccos(y), così come medesime sono le altre considerazioni. Pertanto si ottiene
pY(y) = pX(g1(y))||dg1(y) dy || + pX(g2(y))||dg2(y) dy || = = 2 ⋅ 1 2π ⋅ || − 1 √1 − y2 || = ⎧⎨⎩ 1 π√ 1 − y2 − 1 ≤ y ≤ 1 0 altrove
6.4.2 Caso multidimensionale
Descriviamo questo caso per mezzo del vettore di v.a.
X = (x1, x2, …, xn), a cui è associata una d.d.p. congiunta
pX(x1, x2, …, xn), e di un secondo vettore aleatorio
Y dipendente dal primo mediante la trasformazione
Y = F(X), ovvero
Se esiste la relazione inversa
X = F− 1( Y) = G(Y) univoca, composta dall’insieme di funzioni
xi = gi(y1, y2, …, yn) per
i = 1, 2, ⋯, n, allora per la d.d.p di
Y sussiste un risultato formalmente molto simile a quello valido nel caso monodimensionale, e cioè
in cui
pX(x = G(Y)) è la d.d.p. di
X calcolata con argomento dipendente da
Y, e
|det(J(X ⁄ Y))| è il modulo del
jacobiano della trasformazione inversa
G, ossia del determinante della matrice costituita da tutte le derivate parziali di
G, detta
jacobiana:
J(X ⁄ Y) = ⎡⎣ ∂xi ∂yj ⎤⎦ = ⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣ ∂x1 ∂y1 ∂x1 ∂y2 ⋯ ∂x1 ∂yn ∂x2 ∂y1 ⋱ ⋮ ⋮ ⋱ ⋮ ∂xn ∂y1 ⋯ ⋯ ∂xn ∂yn ⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦
Un esempio di applicazione della teoria appena discussa viene svolta al §
14.4, allo scopo di descrivere in termini probabilistici il problema della detezione di una sinusoide immersa nel rumore; tale descrizione è quindi usata al §
6.6.1 per impostare il problema della decisione statistica. Un altro caso applicativo si riferisce alla d.d.p. del prodotto tra v.a. (pag.
1).