6.5 Gaussiana multidimensionale
Questo termine individua una v.a. vettoriale
X ottenuta a partire da
n v.a. marginali
xi, i = 1, 2, ⋯, n tutte gaussiane. La d.d.p.
congiunta in questo caso è espressa in modo formalmente simile a quello del caso unidimensionale, come
in cui
x = [x1, x2, ⋯, xn] è il vettore riga che rappresenta le
n v.a. marginali,
mx è il vettore dei rispettivi valori medi,
Σx è la
matrice di covarianza (vedi §
7.1.2) i cui
n × n elementi risultano pari a
σxi, xj = E{(xi − mxi)(xj − mxj)}, e
⊤ rappresenta l’operatore di trasposizione. In tal caso le v.a. marginali
xi vengono dette
congiuntamente gaussiane, e la conoscenza di
mx e
Σx ne definisce in modo
completo la densità di probabilità. Per un approfondimento delle proprietà analitiche di
Σx, si veda il §
6.7.3.
Notiamo che il termine
1⁄√(2π)ndet(Σx) rappresenta l’altezza di
pX(x) per
x = mx, in cui l’esponente di
(10.136) si annulla. Per
x ≠ mx lo stesso esponente è una
forma quadratica (pag.
1) sempre positiva, e che cresce all’aumentare di
|x − mx|.
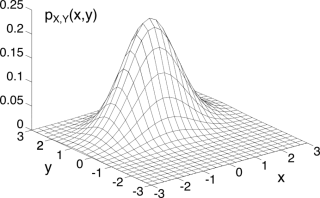
Esempio In figura
6.14-a) è rappresentato il grafico
3d di una d.d.p. gaussiana bidimensionale
pXY(x, y), con
m = (0, 1) e
Σ = ⎡⎢⎣ 1 0.1 0.1 0.5 ⎤⎥⎦: si può notare l’asimmetria legata ai valori
σ2x ≠ σ2y, e la centratura dovuta ad
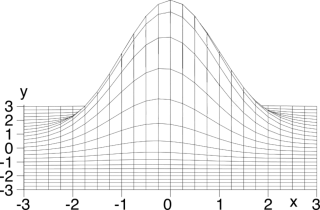
my ≠ 0. La fig.
6.14-b) mostra la stessa d.d.p. da un punto di vista corrispondente agli assi, mentre la fig.
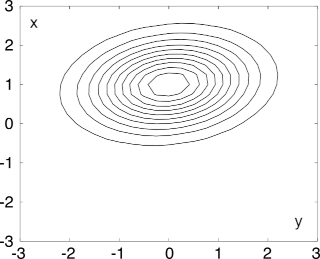
6.14-c) ne riporta le
curve di livello, che mostrano come la forma quadratica dell’esponente determini per la superficie di
pXY(x, y) dei contorni
ellittici, in cui la lunghezza degli assi delle ellissi è legata a
σx e
σy, mentre l’inclinazione dipende dalla covarianza
σxy.
6.5.1 Indipendenza statistica per v.a. gaussiane incorrelate
Affrontiamo la dimostrazione di quanto affermato in fondo al §
7.1.2, ovvero che,
unicamente nel caso di v.a. congiuntamente gaussiane, il sussistere di incorrelazione tra le stesse ne implica l’indipendenza statistica. Osserviamo infatti che nel caso in cui le v.a. marginali siano incorrelate, ossia
σxixj = 0 con
i ≠ j, la matrice di covarianza
Σx risulta essere
diagonale, così come la sua inversa, i cui elementi risultano in tal caso essere pari a
1⁄σ2xi; inoltre, si ottiene che
det(Σx) = ∏ni = 1σ2xi. Pertanto in questo caso la
(10.136) si esprime come
che evidentemente equivale al
prodotto delle singole d.d.p. marginali
p(xi) = 1√ 2π σxi exp⎧⎩− 1 2 (xi − mxi)2σ2xi ⎫⎭
Ma dato che questo risultato è proprio la definizione di indipendenza statistica (§
7.1.2) tra le v.a. marginali, abbiamo ottenuto la dimostrazione cercata.
Infine, osserviamo che nel caso in cui le v.a. marginali siano indipendenti, eguagliando l’esponente della
(10.137) ad una costante si ottiene l’equazione di una ellisse riferita agli assi principali, ossia le curve di livello di fig.
6.14-c) si dispongono con gli assi paralleli a quelli del dominio descritto dal vettore aleatorio x. 6.5.2 Trasformazione lineare di v.a. gaussiane
Un’altra importante proprietà di questo tipo di v.a. è la sua
invarianza rispetto alle operazioni di combinazione lineare. Se infatti indichiamo con
X una v.a. gaussiana multivariata, e con
Y = XA un secondo vettore aleatorio ottenuto mediante moltiplicazione di
X per una matrice
A, fornendo
yj = ∑ni = 1aijxi, possiamo mostrare che anche
Y risulta descrivere una v.a. gaussiana. In accordo con la trattazione svolta al §
6.4.2, scriviamo la trasformazione inversa come
X = YB in cui
B = A− 1, mentre per la d.d.p. della nuova v.a.
Y, in base alla
(10.135) otteniamo
pY(y) = pX(x = yB) ⋅ det(B), in quanto la matrice jacobiana
J(X ⁄ Y) corrisponde alla trasposta della matrice
B stessa; inoltre, risulta che
mx = myB. Sostituendo questi risultati nella
(10.136) si ottiene pertanto
pY(y) = det(B) √(2π)ndet(Σx) exp⎧⎩− 1 2 ( yB − myB) Σ− 1x (yB − myB)⊤⎫⎭ = det(B) √(2π)ndet(Σx) exp⎧⎩− 1 2 ( y − my) BΣ− 1xB⊤ (y − my)⊤⎫⎭
che è nuovamente l’espressione di una d.d.p. gaussiana multivariata
y, con media
my = mxB− 1 = mxA e covarianza
Σy = A⊤ΣxA.
6.5.3 Processo gaussiano
Una importante classe di segnali aleatori è costituita da un processo stazionario in senso lato, la cui d.d.p. di primo ordine è gaussiana, e dai cui membri è possibile estrarre ad istanti diversi una o più v.a. gaussiane, che indichiamo collettivamente con il vettore aleatorio
x, descritto dalla d.d.p. multivariata
(10.136).
La stazionarietà garantisce che il corrispondente vettore dei valori medi
mx presenti tutti gli elementi uguali e pari a
mx = E{x(t)}, e che la matrice di covarianza
Σx presenti elementi ottenuti valutando la covarianza
σx(τ) = E{(x(t) − mx)(x(t + τ) − mx)} del processo (vedi eq.
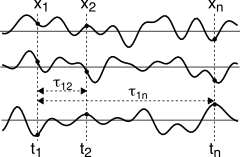
10.152) in corrispondenza degli intervalli temporali
τij tra gli istanti di campionamento nei quali sono estratte le coppie di v.a. marginali
xi e
xj descritte dalla gaussiana multivariata. In altre parole, i valori
σij che compaiono in
Σx sono ottenuti come
σij = σx(τij), mentre su tutta la diagonale compare la varianza
σ2x = σx(0).
Essendo il processo gaussiano, le due grandezze
mx e
Σx lo descrivono completamente, e se si verifica anche l’ipotesi di ergodicità, possono essere stimate a partire da una qualunque realizzazione, vedi eq.
(10.138) a pag.
1.