15.5 Ricevitore ottimo

In questa sezione rimettiamo in discussione i risultati ottenuti ai §§ 15.2.2.3 e 15.4.5. 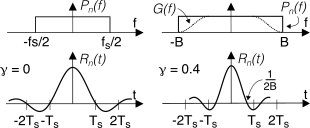Infatti come è stato illustrato al § 7.6 in relazione al filtro adattato in presenza di rumore bianco, il valore di SNR al punto di decisione è massimo se si usa un filtro di ricezione h_R(t) adattato alla forma dell’impulso trasmesso g(t) = h_T(t), ovvero (a meno di traslazioni temporali) per il quale risulti H_R(f) = G^*(f). Al contrario, nello schema adottato per la figura a pag. 1 il filtro di ricezione ha l’unico scopo di limitare la banda del rumore, ed è sempre un passa-basso ideale, indipendentemente dalla scelta fatta per g(t). In tal caso, se si adotta una G(f) di Nyquist non a banda minima, i campioni di rumore (sovrapposti a quelli di segnale) danno luogo a v.a. x(kT_s) gaussiane ma non più indipendenti [765]   [765]  Infatti il segnale n(t) uscente da H_R(f) = rect_2B(f) ha autocorrelazione R_N(τ) = F ⁻¹{|H_R(f)|²} = 2B sinc(2Bτ) (vedi § 7.2.4), che passa da zero per τ = 12B.

Se si utilizza una G(f) a coseno rialzato con γ > 0 occorre estendere la banda di ricezione a B = f_s2(1 + γ), a cui corrispondono campioni di rumore incorrelati se prelevati a distanza multipla di τ = 12B = 1f_s(1 + γ), mentre invece il segnale è campionato con frequenza pari a quella di simbolo f_s, e dunque con campioni a distanza τ = T_s = 1f_s. Pertanto i campioni di rumore sono correlati, con autocorrelazione pari a R_N(T_s) = 2B sinc(1 + γ).

, e quindi la P_e che si ottiene non è la minima possibile [766]   [766]  Al § 6.5.1 si dimostra come delle v.a. gaussiane incorrelate siano anche statisticamente indipendenti, mentre nel nostro caso i campioni di rumore sono correlati, e statisticamente dipendenti. In accordo alla trattazione della regressione (§ 7.7.1) e della predizione lineare (§ 10.1.2.2), osserviamo che la dipendenza statistica tra campioni di rumore implica la possibilità di ridurre l’incertezza relativa ai nuovi valori a partire dalla conoscenza dei valori passati. Il vero valore di un campione di rumore può essere calcolato sottraendo al valore s_k − 1 del segnale ricevuto all’istante di simbolo k − 1, il valore del simbolo deciso senza commettere errore; da questo risultato è possibile predire il successivo campione di rumore come n̂_k = n_k − 1R_N(T_s)R_N(0), che viene quindi sottratto al successivo valore s_k osservato. In tal modo, anche se la regressione non è esatta, l’ampiezza (e la varianza) del rumore residuo sono comunque ridotte, ed altrettanto la probabilità di errore del decisore..

Per rendere incorrelati i campioni di rumore e ridurre la P_e al minimo, realizzando al contempo le condizioni di Nyquist in ricezione, tentiamo di verificare anche le condizioni H_R(f) = H ^* _T(f) di filtro adattato, decomponendo il filtro a coseno rialzato G(f) in parti uguali tra trasmettitore e ricevitore e dando quindi luogo allo schema di figura 15.41, in cui

H_T(f) = H_R(f) = √G(f)

Figure 15.41 Ricevitore ottimo con impulso a radice di coseno rialzato

In tal modo al decisore giunge esattamente lo stesso segnale di prima [767]   [767] Infatti quando G(f) è tutta al trasmettitore il segnale generato (e ricevuto) ha espressione (21.7) (vedi anche la (21.1)); indicando ora g^√(t) = F ⁻¹{√G(f)}, ed eseguendo un calcolo del tutto analogo a quello svolto in § 15.1.2.2, si ottiene che il segnale ricevuto nel caso di scomposizione di G(f) ha espressione

r(t) = h_T(t) * h_R(t) * ∑_k a_k ⋅ δ(t − kT_s) = ∑_k a[k] ⋅ g(t − kT_s)

in quanto h_T(t) * h_R(t) = g^√(t) * g^√(t) = g(t) per la proprietà di prodotto in frequenza.

, mentre la densità di potenza del rumore a valle di H_R(f) non è più costante, ma ora vale

(21.22) P_ν(f) = N₀2 |H_R(f)|² = N₀2 G(f)

Pertanto i campioni di rumore presi a distanza T_s sono incorrelati (e quindi statisticamente indipendenti perché gaussiani, vedi § 6.5.1) in quanto R_ν(τ) = F ⁻¹{P_ν(f)} è ora un impulso di Nyquist, che passa da zero per τ = kT_s. Notiamo che, essendo G(f) reale pari, la fattorizzazione di G(f) realizza effettivamente la condizione H_R(f) = H ^* _T(f) che definisce un filtro adattato.

Figure 15.42 Confronto della risposta impulsiva del filtro ottimo e subottimo

15.5.1 Equalizzazione del ricevitore ottimo

• 1. ricevitore non sia ottimizzato ed il canale sia perfetto;
  2. il filtro a coseno rialzato sia ripartito tra trasmettitore e ricevitore;
  3. sia presente un canale con |H(f)|² = 0.4 ⋅ cos(2π3ff_b) + 0.6 e l’equalizzazione sia tutta al lato trasmittente;
  4. come 3., ma con l’equalizzazione ripartita tra i due estremi del collegamento.
  Svolgimento
  1. - Per il valore di E_bN₀ otteniamo E_bN₀ =  P_xf_b 12P_n(f) = 110⁷ 110^− 8 = 10 pari a 10 dB. Per valutare la P_e utilizziamo la seconda curva di fig.  15.31 che raffigura la (21.21) per γ = 1 ed L = 2 (il nostro caso), ovvero P^bit_e = 12 erfc⎧⎨⎩√E_bN₀ 11.5⎫⎬⎭. Dunque per E_bN₀|_dB = 10 dB troviamo una P_e ≃ 10^− 4;
  2. - siamo nelle condizioni di ricevitore ottimo, e l’espressione della P_e è data dalla (21.24) ovvero (per γ = 1 ed L = 2) P^bit_e = 12 erfc⎧⎨⎩√E_bN₀ 1⎛⎝1 − γ4⎞⎠⎫⎬⎭ = 12 erfc⎧⎨⎩√E_bN₀ 10.75⎫⎬⎭;
  3. - in presenza

  

  di un canale distorcente equalizzato al trasmettitore, il ricevitore ottimo subisce un peggioramento di prestazioni equivalente ad un decremento di E_bN₀|_dB della quantità α_dB = 10log₁₀ ∫^B_− BG(f)|H(f)|²df che, valutata per via numerica con un programmino Octave, risulta pari a circa 3.5 dB; pertanto al nuovo E_bN₀|_dB = 13 − 3.5 = 9.5 dB corrisponde una P_e ≃ 3 ⋅ 10^− 4;
  4. - qualora l’equalizzazione sia ripartita tra i due estremi il decremento equivalente di E_bN₀|_dB è pari alla quantità β_dB = 20log₁₀ ∫^B_− BG(f)|H(f)|df che valutata per via numerica risulta pari a circa 3.15 dB, e quindi al nuovo E_bN₀|_dB = 13 − 3.15 = 9.85 dB corrisponde una P_e ≃ 1.5 ⋅ 10^− 4;

Licenza Creative Commons BY-NC-SA	Ottieni il PDF o la Stampa Storia Blog
	Trasmissione dei Segnali e Sistemi di Telecomunicazione è un progetto ventennale di cultura libera evoluto fino alla forma attuale
Come vedi non c'è traccia di pubblicità, ma in compenso adoriamo le Donazioni