15.6 Gestione degli errori di trasmissione
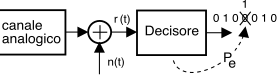
La figura a lato, già proposta a pag.
1, ricorda ancora una volta come le conseguenze prodotte dagli errori del decisore siano alcuni bit
diversi da quelli trasmessi. Al §
15.4.9.2 siamo giunti al calcolo probabilità di errore
Pbite dovuta a rumore additivo, mentre al §
15.2.2.3 è stato illustrato come anche una non perfetta temporizzazione, od una alterazione dell’impulso
g(t), possano causare errori di decisione dovuti all’
isi. Sempre al primo capitolo è anche mostrata la figura riproposta sotto e che illustra come la
Pe, qualunque ne sia la causa, possa essere
ridotta adottando tecniche di
codifica di canale e
controllo di errore, discusse nel seguito.
15.6.1 Controllo di errore
Con questo termine si individuano le strategie atte a
proteggere le informazioni da trasmettere, aumentando il numero effettivo dei bit inviati (che passano da
fb a
f’b > fb bit/secondo, vedi figura), in modo che i bit aggiunti siano
dipendenti dagli altri, permettendo la gestione degli eventuali errori di trasmissione. Vedremo che la quantità di bit aggiunti, indicata anche come
ridondanza (§
390), può essere appena sufficiente a permettere di
accorgersi della presenza di errori di trasmissione, o (se più elevata), può mettere il lato ricevente anche in grado di
correggere fino ad una certa percentuale dei bit errati. Sussistono dunque due diverse modalità di gestione degli errori:
Forward error correction o FEC
Qualora il sistema di trasmissione sia da considerare
unidirezionale, e dunque sprovvisto di un canale di ritorno idoneo a chiedere la
ritrasmissione dei dati errati, l’unica soluzione consiste nell’aggiunta di una ridondanza sufficiente a correggere direttamente la maggior parte degli eventuali errori. La soluzione prende il nome di correzione di errore
in avanti o
fec, e si è sviluppata nel contesto della
codifica di canale (vedi §
15.6.2), appannaggio del mondo delle telecomunicazioni.
Automatic repeat request o ARQ
Se al contrario è presente un canale di comunicazione
a ritroso, e non sussistono rigidi vincoli temporali sul massimo ritardo tra trasmissione e ricezione corretta, allora ci si può accontentare di un minor grado di ridondanza, sufficiente ad
accorgersi degli errori, ovvero a
rivelarli, ma non a correggerli. Infatti è ora possibile invocare la
ritrasmissione del dato errato, dando luogo ad una
strategia di richiesta di ripetizione o
arq (vedi §
22.6): tale approccio si è sviluppato nel contesto delle reti di computer e della trasmissione dati, ed ha dato origine ai
protocolli a finestra (§
23.1.2.3).
Le unità informative su cui operano
fec e
arq in generale non sono singoli bit, ma gruppi di bit denominati
parole o
word, e per questo siamo interessati a valutare come la
Pbite calcolata al §
15.4.9.2 influenzi il
numero di errori in una parola, dato che da ciò dipende la possibilità di rilevarli e/o correggerli.
15.6.1.1 Errori su parole
Occupiamoci quindi di determinare la probabilità
P(i, n) di trovare
0 ≤ i ≤ n bit errati
in una parola di
n bit, qualora ciascun bit possa essere errato con probabilità
p = Pbite e nell’ipotesi che gli eventi di errore siano statisticamente indipendenti (§
6.1.5), ovvero che il verificarsi o meno di un errore su di un bit non condizioni gli altri.
Per i casi
i = 0 (tutti giusti) ed
i = n (tutti sbagliati) il risultato è immediato, in quanto risulta
P(0, n) = (1 − p)n e
P(n, n) = pn. Per
0 < i < n ci troviamo in un classico caso di
prove ripetute, in quanto si tratta di osservare l’evento di errore (con probabilità
p) su
n ripetizioni. La probabilità che ci siano esattamente (ad es. i primi)
i bit errati ha valore
pi(1 − p)n − i, ma dato che i bit errati possono essere comunque distribuiti su
n, e che vi sono
⎛⎜⎝n i⎞⎟⎠ = n(n − 1)⋯(n − i + 1)i! modi di scegliere
i oggetti su
n, il risultato cercato è espresso dalla d.d.p. di Bernoulli (vedi §
22.1)
che, se
np < 0.1, può essere approssimata come
La
(21.27) applicata al caso di un singolo errore (
i = 1) su
n fornisce
P(1, n) ≃ np, ovvero la probabilità di
un solo bit errato
su n è circa pari ad
n volte la
Pbie nel flusso binario. D’altro canto, per la probabilità di
due bit errati su
n la
(21.27) fornisce
P(2, n) ≃ 12 n(n − 1) p2 e, sempre se
np < 0.1, osserviamo che
P(2, n) ≪ np ≃ P(1, n), ovvero inferiore a quella di un solo bit errato. Più in generale, risulta che
e quindi si può considerare la probabilità di ricevere
i o più bit errati su
n, praticamente uguale a quella di osservare solo
i errori. All’aumentare di
p e/o di
n, l’approssimazione perde validità, e la probabilità
P(i, n) può invece
aumentare con
i, e in tal caso il sistema di trasmissione è praticamente inusabile. E’ questo il motivo per cui non è opportuno che la lunghezza
n delle parole ecceda il limite
np < 0.1 imposto dalla probabilità di errore sul bit
p = Pbite offerta dal collegamento.
L’esposizione prosegue introducendo per prime definizioni e soluzioni che realizzano la
correzione degli errori, il cui approfondimento è svolto al §
17.4, mentre al §
15.6.3 sono illustrate tre tecniche comunemente utilizzate per la
detezione di errore; la descrizione dei protocolli
arq è infine rimandata al §
22.6.
15.6.2 Correzione di errore e codifica di canale
Affrontiamo i criteri con cui scegliere i bit di ridondanza allo scopo di realizzare un sistema di tipo
fec basato sulle tecniche di
codifica di canale, peraltro idonee ad essere utilizzate anche per il caso dei sistemi
arq. Descriviamo quindi due semplici metodi di correzione di errore, ossia il
codice a ripetizione e
l’interleaving.
La
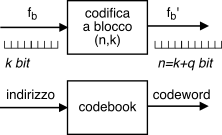
codifica a blocco opera raggruppando
k bit consecutivi del messaggio originale, distinti dai precedenti e dai successivi blocchi di
k. Per ogni
k bit da trasmettere il codificatore produce
n = k + q bit in uscita che sono trasmessi al posto dei
k di ingresso, da cui dipendono in modo univoco.
L’operazione di
mappatura svolta dal codificatore può essere pensata o realizzata come l’accesso ad una tabella (o memoria) denominata
codebook (o
cifrario), dove i
k bit da codificare rappresentano un
indice che individua
2k differenti righe, in cui si trovano scritte le
parole di codice (
codeword), costituite ognuna da
n = k + q bit. Un codice siffatto è detto
codice (n, k).
Esprime la proporzione percentuale tra il numero dei
q bit di protezione aggiunti rispetto ai
k (di informazione) in ingresso al codificatore, ovvero
ρ = qk ⋅ 100 %
ed è una misura del grado di protezione offerto dal processo di codifica.
Esempio In una trasmissione con ridondanza del 50% per ogni coppia di bit di informazione ne viene inserito uno di protezione.
La presenza di ridondanza fa sì che il numero 2k di codeword esistenti sia inferiore a quello delle 2n possibili configurazioni di n bit, in modo che se un bit di una codeword viene modificato a causa di un errore del decisore, la nuova parola di n bit individua una configurazione che nel codebook non esiste, permettendo così di rivelare e/o correggere l’errore. Ma cosa succede se avviene più di un errore per codeword? Per rispondere, introduciamo un nuovo concetto:
E’ indicata come
dH(ci, cj) e misura la
dissimilarità tra due codeword
ci, cj, espressa come il numero di posizioni di bit in cui esse sono diverse. Viene calcolata eseguendo
l’or esclusivo delle rispettive rappresentazioni binarie, e contando il numero di
uni del risultato.
Esempio Con
ci = 011010 e
cj = 010110 si ottiene il risultato mostrato a lato,
che evidenzia come le codeword differiscano in due posizioni di bit, e dunque
dH(ci, cj) = 2.
Individua la
minima distanza di Hamming
dm tra tutte le possibili coppie di codeword di uno stesso codebook
dm = mini ≠ j dH(ci, cj)
e permette di valutare la capacità di rivelazione e correzione del codebook, in quanto rappresenta il minimo numero di errori necessario a trasformare una codeword in un’altra, almeno nel caso peggiore di due parole a distanza
dm.
Rivelazione e correzione di errore
Un codice con distanza dm può
- rivelare al massimo dm − 1 errori, in quanto se ne avvengono di più si finisce in un’altra codeword, e
- correggere fino a dm − 12 errori, oltre i quali si finisce più vicini ad una altra codeword.
Mentre la prima azione è possibile ogniqualvolta si osservi una codeword
cα non presente nel codebook, per intraprendere la seconda occorre operare una decisione relativa a quale sia la codeword
ĉ realmente trasmessa in base ad un criterio di
minima distanza, ovvero scegliendo la codeword più vicina (nel senso della distanza di Hamming) a quella ricevuta:
ĉ = argminci dH(ci, cα)
Esempio Nel caso in cui dm = 3, la presenza di un solo bit errato su n fa sì che la codeword ricevuta differisca da quella trasmessa per un bit, mentre mantiene almeno due bit di differenza rispetto a tutte le altre possibili, permettendo così al ricevitore di correggere l’errore. Se sono invece presenti due errori, la parola ricevuta diviene più vicina ad una codeword diversa da quella trasmessa, ed in tal caso la procedura di correzione sceglierebbe una codeword errata.
E’ quindi un po’ come se attorno ad ogni codeword fosse costruita una sfera contenente tutte le parole di n bit che non sono codeword e che sono distanti dalla codeword al massimo dm − 12 bit: la ricezione di ciascuna di esse comporta la decisione per la codeword al centro della sfera.
Per un generico codice a blocco
(n, k) la distanza
del codice dm rispetta la diseguaglianza
dm ≤ q + 1
ovvero
dm ≤ n − k + 1 dato che
n = k + q. Infatti i
2k bit da proteggere sono qualunque, e dunque il contributo di questi
k bit alla distanza tra codeword è uno; tale distanza può aumentare al massimo di una ulteriore unità per ognuno dei
q bit aggiunti.
Esempio Aggiungendo
q = 3 bit di ridondanza si ha
dm ≤ q + 1 = 4, e se per una particolare scelta del codebook (ad es. di Hamming, §
17.4.1.1) si ottiene
dm = 3, saremo in grado di correggere un errore e rivelarne 2.
Probabilità di errore residua per codeword
Da quanto illustrato fin qui occorre stabilire
a priori se utilizzare il codice a fini di correzione oppure di detezione. Indicando con
eM il massimo numero di errori che è possibile correggere o rivelare, può essere definita una probabilità
residua di errore
su parola Pre per descrivere il caso in cui, anche dopo l’esecuzione delle procedure di controllo di errore, siano ancora presenti errori, perché in numero superiore ad
eM e dunque eccedenti la capacità correttiva del codice. Risulta quindi che
Pre = P(i > eM, n) che, nelle condizioni di validità della
(21.27), è pari a
P(eM + 1, n). In linea generale, la
valutazione dell’errore residuo
sul bit dipende dal tipo di controllo di errore attuato.
L’efficienza del codice è misurata dal
tasso di codifica (code rate)
Rc = kn < 1
che rappresenta la frazione di bit informativi sul totale di quelli trasmessi, e che consente di scrivere la velocità di uscita dal codificatore come
Esempio In una trasmissione con un tasso di codifica pari a 0.5, il numero di bit uscenti (per unità di tempo) dal codificatore di canale è il doppio del numero dei bit entranti.
L’argomento dei codici a blocco è molto vasto, e fornisce molteplici soluzioni, la cui trattazione esauriente eccede il livello di approfondimento del presente capitolo (vedi però il §
17.4.1); gli stessi tre casi di controllo di errore trattati al §
15.6.3 (parità, somma di controllo e
crc) possono essere inquadrati nel contesto dei
codici a blocco. Qui ci limitiamo ad un esempio di codice a correzione molto elementare, il codice
a ripetizione, mentre al §
17.4.1.1 è illustrata una tecnica nota come codice
di Hamming, in grado di conseguire una efficienza di gran lunga migliore.
15.6.2.2 Codice a ripetizione n:1
Realizza un codice a blocco molto semplice e con proprietà correttive, per il quale
k = 1 e le uniche due codeword sono di
n bit tutti uguali al bit in ingresso; ponendo ad esempio
n = 3 si ottiene il codice
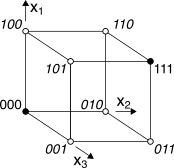
a ripetizione 3:1, con codeword 000 ed 111, di cui in
figura è riportata la disposizione (rappresentate come pallini) in uno spazio vettoriale descritto dai tre bit di codice
x1x2x3, ed in cui i cerchi vuoti indicano gli 8-2=6 vettori binari che
non sono codeword, scritti in
corsivo. Se gli errori sono sufficientemente distanti nel tempo la correzione può basarsi su di una “votazione a maggioranza” (
majority voting): sempre nel caso di
n = 3 si ottiene
dm = 3, ed il codice è in grado di correggere un errore e rivelarne due.
Notiamo come questo codice sia particolarmente poco efficiente, dato che per esso si ottiene un tasso di codifica Rc = kn = 1n; d’altra parte, il codice a ripetizione è uno dei pochi per cui dm = q + 1, e non meno.
Esercizio Calcolare la probabilità di errore residua
Pr per un codice a ripetizione 3:1, in presenza di una
Pbite = p.
Risp. Come discusso il codice può correggere un errore singolo, mentre in presenza di un errore doppio la decisione a maggioranza modifica anche il terzo bit, ed un errore triplo passa inosservato. La
(21.27) approssima la probabilità che due o più bit su tre siano errati come
P(2, 3) ≃ 123 ⋅ 2p2 = 3p2 che è la
Pr cercata
per codeword. Dato che per il codice a ripetizione ad ogni codeword corrisponde un solo bit del messaggio originario, lo stesso valore di
Pr = 3p2 è anche la
Pbite residua. Ad esempio, in corrispondenza di una
p = 10 − 4 iniziale, dopo decodifica si ottiene una
Pbite = 3 ⋅ 10 − 8.
Compromesso banda - potenza
Torniamo su questo argomento (§
15.4.7) in quanto l’adozione di un codice di canale aumenta di fatto la
fb eq.
(21.29) e dunque l’occupazione di banda eq.
(21.5); non solo, ma a parità di potenza
Px ricevuta l’aumento di
fb comporta la riduzione di
Eb = Px⁄fb e dunque di
Eb⁄N0 della stessa frazione, e quindi un
peggioramento della
Pe di base su cui opera il decodificatore di linea. Evidentemente il miglioramento apportato dalla codifica
fec sopperisce anche al peggioramento dovuto all’aumento di banda, che la teoria dell’informazione prevede possa essere ripagato da un minor bisogno di potenza per ottenere le stesse prestazioni.
Esercizio Proseguendo l’esercizio precedente, osserviamo che il codice a ripetizione determina una
fb tripla, e dunque un
Eb⁄N0 ridotto di un terzo, ovvero di circa -4.7 dB inferiore rispetto al caso non codificato. Dalle curve di fig.
15.39 riscontriamo che il miglioramento sulla
Pe (da
104 a
3 ⋅ 10 − 8) dovuto al codice corrisponde più o meno allo stesso numero di dB. Per codici più efficienti (con minore aumento di banda come ad esempio il codice di Hamming, vedi §
17.4.1.1) il bilanciamento tra i due effetti conferma il risultato anticipato dal compromesso banda-potenza, qui applicato alla codifica di canale.
Le capacità di correzione fino ad ora discusse sono valide purché gli eventi di errore siano
statisticamente indipendenti. In realtà gli errori possono presentarsi in maniera
non indipendente, e concentrati in un breve intervallo di tempo: questa circostanza è indicata come
caso degli errori a pacchetto . In tal caso, si usa ricorrere alla tecnica nota come
scrambling o
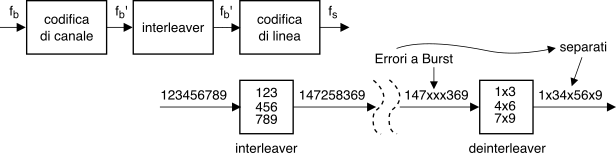
interleaving attuabile a patto di accettare un ritardo di trasmissione. Si tratta infatti di modificare l’ordine dei dati inviati, in modo che gli errori che si manifestano su bit
vicini si riflettano in errori su bit...
lontani, e quindi appartenenti a codeword differenti, come illustrato in fig.
15.47 in cui i bit sono scritti per righe e letti per colonne. Una analisi più approfondita viene svolta a pag.
1. Ovviamente, occorre prevedere un processo inverso
(descrambling o
deinterleaving) all’altro capo del collegamento. E’ appena il caso di notare che lo scrambler (similmente al codice di Gray)
non altera il
numero dei bit trasmessi, e dunque
non è una forma di codifica
fec.
La trattazione della codifica di canale di tipo
fec prosegue in modo più approfondito al §
17.4, dove sono illustrate le tecniche più avanzate.
15.6.3 Detezione di errore
In questo caso ci si limita a mettere il ricevitore in grado di accorgersi della presenza di errori, senza poterli correggere. Le parole errate possono essere scartate, oppure può esserne richiesta la ritrasmissione.
15.6.3.1 Controllo di parità
Viene comunemente usato nell’ambito della trasmissione asincrona (§
15.7.1) e sincrona orientata al carattere (pag.
1) per rivelare errori sul bit, e consiste nell’aggiungere alla parola da trasmettere un unico ulteriore bit, in modo che in totale ci sia un numero
pari di uni, applicando così una regola di
parità pari (
even). Il caso opposto, ossia l’aggiunta di un bit in modo da rendere
dispari il numero di uni, prende nome di parità
odd.
In entrambi i casi dopo aver raggruppato i bit pervenuti il ricevitore esegue un
controllo detto appunto
di parità, semplicemente contando il numero di uni, ed accorgendosi così se nella parola si sia verificato un errore (uno zero divenuto uno o viceversa). In tal caso, il ricevitore invierà all’altro estremo del collegamento una richiesta di ritrasmissione del gruppo di bit errato. Se invece si è verificato un errore che coinvolge
due bit della parola, questo passerebbe inosservato, in quanto la parità prescritta verrebbe mantenuta. Infatti, la
distanza di Hamming (vedi pag.
1) relativa ad un codebook ottenuto aggiungendo ad ogni possibile parola di
k bit il corrispondente di parità, è pari a due.
Esempio: indicando la probabilità di errore sul bit con
p (es
10 − 3) ed applicando la
(21.27) si ottiene che la probabilità di
i = 2 errori su
n = 10 bit vale
Pworde = 12 n(n − 1) p2 = 4.5 ⋅ 10 − 5, che rappresenta il
tasso residuo di errore
su parola legato all’uso di un bit di parità: essendo due i bit errati su
10, la
Pbite = P{err ⁄ worde} ⋅ Pworde risulta pari a
210 ⋅ 4.5 ⋅10 − 5 = 0.9 ⋅ 10 − 5, un bel risultato rispetto al
10 − 3 di partenza.
Il concetto di parità può essere esteso calcolando
q bit di parità, ognuno a partire da un
diverso sottoinsieme dei
k bit di ingresso, con sottoinsiemi eventualmente sovrapposti. Un codice del genere prende il nome di codice di
Hamming, descritto al §
17.4.1.1.
15.6.3.2 Somma di controllo o checksum
Quando il messaggio è composto da
M diverse parole di
N bit, la probabilità che almeno una di queste sia errata aumenta in modo circa proporzionale ad
M, in base ad un ragionamento del tutto analogo a quello della nota
778.
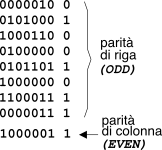
Per aumentare le capacità di rivelazione del controllo di parità applicato sulle singole parole (indicato ora come parità
di riga, o
trasversale), si aggiunge al gruppo di
M parole una ulteriore parola (detta
somma di controllo o
checksum), i cui bit si ottengono applicando il controllo di parità a tutti i bit “omologhi” delle
M parole incolonnate, generando così una parità
di colonna (o
longitudinale), come esemplificato in figura.
A volte, si preferisce calcolare la somma di controllo mediante una operazione di somma modulo uno, direttamente realizzabile in software in modo veloce. In tal caso, il ricevitore calcola una nuova somma di controllo longitudinale, includendo anche la somma di controllo originaria: in assenza di errori, il risultato deve fornire zero.
15.6.3.3 Codice polinomiale e CRC
L’utilizzo di una somma di controllo può produrre risultati scadenti nel caso di una distribuzione temporale dei bit errati particolarmente sfavorevole, mentre la tecnica nota come
Cyclic Redundancy Check (o
crc) garantisce prestazioni
più uniformi.
Questo metodo consiste nell’aggiungere ad una parola
P di
k bit che si desidera trasmettere, un gruppo
R di
q < k ulteriori bit
di protezione, calcolati a partire dai primi
k, in modo da permettere la detezione di eventuali errori; sotto questo aspetto, il
crc rientra nella categoria dei
codici a blocco (§
15.6.2.1).
L’aggettivo
polinomiale trae origine dalla associazione tra un numero binario
B di
n + 1 bit, indicati con
bi,
i = 0, 1, …n, ed un polinomio
B(x) a coefficienti binari nella variabile
x, di grado
n, con espressione
B(x) = bnxn + bn − 1xn − 1 + … + b1x1 + b0
Un
codice polinomiale è definito a partire da un
polinomio generatore G(x) di grado
q, i cui coefficienti binari identificano una parola
G = gqgq − 1…g1g0 di
q + 1 bit.
Indicando ora con
P la sequenza dei
k bit
pi da proteggere,
aggiungiamo a destra di questi un gruppo di
q bit pari a zero, ottenendo una nuova parola
P ⋅ 2q lunga
k + q bit, che quindi dividiamo per
G (mediante aritmetica modulo due), ottenendo un quoziente
Q, ed un resto
R con al massimo
q bit. Pertanto, possiamo scrivere
P ⋅ 2qG = Q ⊕ RG
Le sequenze
Q ed
R costituiscono rispettivamente i coefficienti dei polinomi quoziente
Q(x) e resto
R(x), ottenibili dalla divisione di
P(x) ⋅ 2q per
G(x). I
q bit
R del resto sono quindi utilizzati come
parola di protezione, in modo da esprimere la sequenza
T da trasmettere come
T = P ⋅ 2q ⊕ R di
k + q bit, ovvero con i
k bit più significativi pari a
P ed i
q bit in coda pari ad
R. Il ricevitore effettua anch’esso una divisione, stavolta tra
T e
G, che in assenza di errori produce un
resto nullo
TG = P ⋅ 2q ⊕ RG = P ⋅ 2qG ⊕ RG = Q ⊕ RG ⊕ RG = Q
in quanto sommando in aritmetica modulo due un numero per se stesso, si ottiene un risultato nullo. Pertanto, se
T⁄G = Q con resto nullo, la parola
P è riottenuta semplicemente shiftando
T a destra di
q posizioni.
Nel caso invece in cui si siano verificati errori, indichiamo con
E la sequenza binaria di errore, di lunghezza
k + q bit, ognuno dei quali è pari ad uno se in quella posizione si verifica errore, o zero in caso contrario, in modo da rappresentare il segnale ricevuto
R come
R = T ⊕ E. Se
E ≠ 0 la divisione operata al ricevitore ora fornisce
e quindi si verifica la presenza di un resto diverso da zero, che indica appunto la presenza di errori, tranne nei casi in cui
E risulti perfettamente divisibile per
G, evento con bassa probabilità se
G è scelto opportunamente. Nel caso in cui
q = 1 si ricade nel caso del controllo di parità (§
15.6.3.1), a cui corrisponde
G(x) = x + 1.
Per applicare il metodo, sia il trasmettitore che il ricevitore devono utilizzare lo stesso generatore G(x), per il quale esistono diverse scelte standardizzate. Si può dimostrare che scegliendo G(x) in modo opportuno, il metodo discusso permette di rivelare
- tutti gli errori singoli;
- se G(x) contiene il temine noto + 1, tutti gli errori a burst che si estendono per q o meno bit;
- se x + 1 è un fattore di G(x), tutti gli errori in numero dispari;
- se G(x) è un polinomio primitivo, tutti gli errori doppi;
- se G(x) è un polinomio primitivo di grado q − 1 moltiplicato per il fattore x + 1, tutti gli errori doppi entro un intervallo di 2q − 1 − 1 bit, e tutti gli errori in numero dispari.
L’aspetto che ha reso popolare questo metodo è la maniera in cui è possibile calcolare i
q bit di controllo, che vengono essi stessi indicati come
crc. Infatti la divisione binaria illustrata alla nota
795 è realizzabile a livello circuitale in modo relativamente semplice.
Si tratta di utilizzare un registro a scorrimento
controreazionato (vedi figura seguente), in cui i
k bit da proteggere sono immessi ad uno ad uno da destra verso sinistra,
seguiti da
q zeri consecutivi. Per ogni valore immesso, quelli già presenti
scorrono a sinistra nel registro, ed il bit che
trabocca, oltre a rappresentare una cifra del quoziente, alimenta gli
or esclusivi presenti nel registro; questi ultimi sono posti in corrispondenza dei coefficienti di
G(x) pari ad uno, tranne che per quello corrispondente ad
xq.
Al termine dell’inserimento dei
k + q bit di
P ⋅ 2q, lo stato del registro a scorrimento costituisce proprio il resto
R, da usare come
crc. L’esempio in figura rappresenta il caso mostrato alla nota
795, in cui di
G(x) = x4 + x3 + 1: con un po’ di pazienza, è possibile verificare che il circuito effettivamente svolge i calcoli prescritti dalla procedura di divisione, e che si ottiene lo stesso risultato.