Sezione 7.5: Operazioni elementari sui segnali Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.7: Appendici 

7.6 Filtro adattato

Dopo aver illustrato le trasformazioni subite da un segnale generico che attraversa un filtro generico, affrontiamo lo studio di un caso in cui il filtro viene progettato per essere al servizio di uno specifico segnale.
Allo scopo di anticipare come va a finire, diciamo subito che questa tecnica è un modo per calcolare l’intercorrelazione Ryg(τ) tra il segnale (rumoroso) in ingresso y(t) e quello g(t) che ci aspettiamo di ricevere in assenza di rumore. Tale compito è svolto mediante un filtro [391]   [391] Sfruttando le analogie tra integrale di convoluzione e calcolo dell’intercorrelazione, vedi § 7.1.4. detto appunto adattato a g(t) e posto all’ingresso ad un detettore di impulso, ovvero un dispositivo che deve decidere per la presenza o l’assenza di una forma d’onda nota immersa nel rumore, in modo da rendere minima la probabilità di sbagliare. Un problema simile verrà affrontato al § 14.4.2 in relazione alla detezione incoerente di sinusoide, mentre ora ci riferiamo ad una detezione coerente, ovvero in cui il segnale è completamente specificato, compresa la sua temporizzazione o fase.
Schema di trasmissione
figure f7.155.png
Figure 7.14 Detezione di impulso mediante filtro adattato
Indichiamo il segnale trasmesso come x(t), ottenuto facendo transitare un impulso δ(t) attraverso un filtro con risposta impulsiva hT(t) = g(t), con durata limitata 0 < t < T. Viene ricevuto il segnale y(t), somma di x(t) (presente o meno) e di un processo gaussiano bianco a media nulla n(t), indicato come rumore, con densità spettrale PN(f) = N0 2 .
Decisore a soglia
Un ricevitore basato sul filtro adattato effettua una decisione di massima verosimiglianza (vedi § 6.6.2.1) a riguardo della presenza (ipotesi H1) o assenza (ipotesi H0) del segnale x(t) in base all’osservazione della grandezza z(T) ottenuta (vedi figura 7.14) campionando all’istante t = T l’uscita z(t) del filtro di ricezione HR(f), che opera sul segnale ricevuto y(t). Il valore osservato per z(T) è quindi confrontato con una soglia λ, determinando la decisione per H1 o H0 a seconda se λ sia superata o meno, e commettendo errore sia nel decidere per H1 in assenza di segnale, sia decidendo per H0 in sua presenza [392]   [392] Indicando rispettivamente con Pe0 e Pe1 i due tipi di errore, pari a (vedi fig. 7.16)
Pe0 = ∫∞λpZ(z ⁄ H0)dz e Pe1 = ∫λ−∞pZ(z ⁄ H1)dz
la probabilità di errore complessiva vale Pe = Pe0P0 + Pe1P1, in cui Po = Pr(H0) e P1 = Pr(H1).
.
Legame tra i filtri di trasmissione e ricezione
Alla nota 399 si dimostra che la probabilità di errore del decisore viene resa minima se HR(f) è realizzato in modo che risulti
(10.172) HR(f) = G*(f) e −j2πfT
a cui corrisponde una risposta impulsiva
figure f7.156.png
hR(t) esprimibile come  [393]   [393] Potendo scrivere G * T(f)e −j2πfT = (G(f)e j2πfT)* e ricordando la proprietà (10.41) espressa a pag. 1 F −1{X*(f)} = x*(−t), dalla (10.172) otteniamo
hR(t)  =  F −1{HR(f)} = F −1{G*(f)e −j2πfT} = F −1{(G(f) e j2πfT)*} =         =  g*(θ + T)|θ = − t = g*(T − t)
(10.173)
hR(t) = g*(T − t)
risultato che, nel caso di g(t) reale come in fig. 7.14, corrisponde ad una hR(t) ottenuta ribaltando g(t) rispetto all’asse delle ordinate, e ritardando il risultato di T, in modo da pervenire ad una hR(t) causale.
Prima di individuare il valore da utilizzare per la soglia λ, valutiamo le caratteristiche statistiche dei possibili valori per z(T) in uscita da hR(t), che a causa della presenza del rumore, è una realizzazione di variabile aleatoria.
Segnale assente
In questo caso (ipotesi H0) nel segnale ricevuto è presente solo rumore, ovvero y(t) = n(t), e dunque la grandezza di decisione z(T) è una v.a. gaussiana [394]   [394] Ricordiamo (vedi § 7.4.2) che l’uscita di un filtro al cui ingresso è posto un processo gaussiano, è anch’essa gaussiana. il cui valore si calcola come
zH0(T) = ∫∞−∞hR(τ)y(T − τ)dτ = ∫T0g*(T − τ)n(T − τ)dτ = RGN(0)
ossia è pari all’intercorrelazione (eq. 10.156) calcolata nell’origine tra g(t) ribaltata ed una finestra di una realizzazione del processo n(t). Indicando con mH0z(T) il valore atteso di z(T), troviamo  [395]   [395] Infatti
mHoz(T) = E{z(T) ⁄ H0} = E{RGN(0)} = E{ ∫T0g*(t)n(t)dt} = ∫T0g*(t)E{n(t)}dt
pari a zero se E{n(t)} = 0.
che mH0z(T) = 0, mentre la varianza di z(T) vale  [396]   [396] Dato che mH0z(T) = 0, risulta σ2z(T) = E{z2(T)} =  RZ(τ)|τ = 0. Sappiamo inoltre che
RZ(τ) = RN(τ) * RHR(τ) = N0 2 δ(τ) * RHR(τ) = N0 2 RHR(τ)
pertanto
σ2z(T) =  RZ(τ)|τ = 0 = N0 2 RHR(0) = N0 2 ∫∞−∞h * R(t)hR(t)dt = N0 2 EG
dato che hR(t) ha la stessa energia di g(t).
σ2z(T) =  N0 2 EG, in cui EG è l’energia dell’impulso g(t).
Segnale presente
Se invece il segnale è presente (ipotesi H1) allora y(t) = g(t) + n(t), e si ottiene
zH1(T) = ∫∞−∞hR(τ)y(T − τ)dτ = ∫T0g*(T − τ) [g(T − τ) + n(T − τ)] dτ = 
 = ∫T0g*(T − τ)g(T − τ)dτ + ∫T0g*(T − τ)n(T − τ)dτ =
 = RG(0) + RGN(0) = EG + RGN(0) 
producendo ancora una grandezza di decisione z(T) gaussiana, con la stessa σ2z(T) =  N0 2 EG (dovuta al rumore) ma con valor medio mH1z(T) = EG ≠ 0, dovuto alla presenza di segnale [397]   [397] Infatti, ora risulta mH1z(T) = E{RG(0) + RGN(0)} = EG + E{RGN(0)} in cui il secondo termine è nullo come già osservato, mentre il primo è un valore certo, pari all’energia EG = RG(0) dell’impulso g(t).
Per ciò che riguarda σ2z(T), osserviamo che zH1(T) = EG + zH0(T), dunque le v.a. centrate sono le stesse, e così la varianza σ2zH1(T) = σ2zH0(T) = N0 2 EG : infatti la componente aleatoria dell’uscita è dovuta al solo n(t).
. Notiamo esplicitamente che mH1z(T) = EG non dipende dalla particolare g(t) adottata, né dalla sua durata T, ma solo dalla sua energia, proprio in virtù dell’aver adottato in ricezione un filtro adattato a quello di trasmissione.
Soglia di decisione
La figura 7.16
figure f7.157.png
Figure 7.16 D.d.p. condizionate e
soglia di decisione
mostra l’esito dei nostri calcoli nella forma della d.d.p. della v.a. z(T) nelle ipotesi H0 ed H1, e pertanto il criterio di massima verosimiglianza (vedi § 6.6.2.1) individua come soglia di decisione ottima il valore λ = EG2, a cui compete una probabilità di errore Pe minima qualora Pr(H0) = Pr(H1), ovvero se la probabilità a priori delle due ipotesi è uguale, vedi nota 392.
Ottimalità
Mostriamo ora che il risultato ottenuto permette la migliore separazione tra le d.d.p. condizionate alle due ipotesi, nel senso che qualsiasi altra scelta per HR(f) ≠ G*(f)e −j2πfT con energia EHR = EG avrebbe prodotto delle d.d.p. più ravvicinate. La separazione tra le gaussiane è legata [398]   [398] Il rapporto mH1z(T)⁄σz(T) confronta l’uscita attesa mH1z(T) = E{RGHR(0)} di HR per t = T nell’ipotesi H1, che dipende dall’energia mutua tra g(t) ed hR(t), con la sua deviazione standard σz(T) =  N0 2 RHR(0) dovuta al rumore. al rapporto mH1z(T)⁄σz(T) che viene reso massimo  [399]   [399]  Consideriamo il caso di avere una HR(f) generica. In presenza di solo segnale, si ottiene
|z(T)|2 = | F− 1{Z(f)}|t = T|2 = | ∫∞−∞HR(f)G(f) e j2πfTdf|2
A questa espressione può essere applicata la diseguaglianza di Schwartz (a pag. 1 si enuncia la relazione | ∫∞−∞a(θ)b*(θ)dθ|2 ≤ ∫∞−∞|a(θ)|2dθ ⋅ ∫∞−∞|b(θ)|2dθ, con l’eguaglianza solo se a(θ) = k ⋅ b(θ)), qualora si faccia corrispondere HR(f) ad a(θ), e G(f)e j2πfT a b*(θ), ottenendo così
|z(T)|2 = (mH1z(T))2 ≤ ∫∞−∞|HR(f)|2df ⋅ ∫∞−∞|G(f)|2df
con l’eguaglianza solo se HR(f) = kG*(f) e −j2πfT, ovvero se hR(t) = kg(T − t) (eqq. (10.172) e (10.173)), ossia se HR(f) è adattata a G(f). Scegliendo k = 1, i due integrali a prodotto hanno lo stesso valore, pari a EG, e dunque (mH1z(T))2 = |z(T)|2 = E2G.
dalla scelta (10.172), che porta a mH1z(T) = EG = max. Il quadrato (mH1z(T)⁄σz(T))2 del rapporto suddetto viene indicato anche come rapporto segnale rumore all’istante di decisione [400]   [400] In effetti la (10.174) non è adimensionale ma è esprimibile come [sec], dunque non è un vero e proprio SNR, ma dato che il termine rende l’idea, questa accezione è entrata nell’uso comune., e qualora HR(f) sia adattato vale
(10.174) SNRFA = (EG)2 N0 2 EG  =  2EG N0
Anticipiamo subito la (10.174) è valida solo in presenza di rumore bianco, mentre se questo è colorato, l’SNR diminuisce, ed il filtro ottimo va determinato nel modo specificato poco più avanti.
Esempio Applichiamo i risultati fin qui ottenuti al caso in cui si utilizzi la
figure f7.157-bis.png
g(t) mostrata a lato, in cui poniamo A = 2 e T = 10− 1. Un decisore a filtro adattato sarà allora caratterizzato dalla risposta impulsiva hR(t) mostrata a fianco di g(t). Se campioniamo l’uscita z(t) di hR all’istante t = T, nel caso di assenza di rumore e presenza di segnale, si ottiene il valore
mz =  z(t)|t = T =  g(t) * hR(t)|t = T = ∫T0g(τ)hR(T − τ)dτ
Dato che hR(T − τ) = g(τ),
figure f7.157-bis-a.png
come rappresentato nella figura a lato, allora mz = ∫T0[g(τ)]2dτ = EG, pari a
EG = ∫T0[g(t)]2dt = A2 ∫T0dt = A2T = 4 ⋅ 10− 1.
Il valore di mz = EG rappresenta il contributo di segnale all’uscita, indipendente dal rumore.
Consideriamo ora in ingresso a hR anche un processo di rumore gaussiano ergodico bianco, a media nulla, e densità di potenza Pn(f) = N0 2  =  1 2 10− 1. Il valore atteso mH1z(T) dell’uscita campionata rimane lo stesso mz = EG, ma ora ad esso si sovrappone la componente aleatoria dovuta al rumore, anch’essa gaussiana e caratterizzata da una varianza pari a
σ2z =  N0 2 EG = N0 2 A2T = 1 2 ⋅ 10− 1 ⋅ 4 ⋅10− 1 = 2 ⋅ 10 − 2
Le d.d.p. condizionate mostrate in fig.  7.16 hanno dunque espressione
p(z ⁄ H0) = 1√ 2π σz e −  z2 2σ2z                 p(z ⁄ H1) = 1√ 2π σz e −  (z − mz)22σ2z
in cui σz = √σ2z = √0.02 = 1.41 ⋅ 10− 1, mz = EG = 4 ⋅ 10− 1, mentre per la soglia di decisione, si trova il valore λ = EG⁄2 = 2 ⋅ 10− 1.
Integrate and dump
Si tratta di una soluzione circuitale [401]   [401] Vedi ad es. https://en.wikipedia.org/wiki/Op_amp_integrator in grado di conseguire le prestazioni di detezione del filtro adattato nel caso di un g(t) =  rectT(t), a cui
figure f7.157b.png
corrisponde una hR(t) anch’essa rettangolare. Infatti, il segnale in uscita vale
vo(t) = − 1 RC t⌠⌡0 vi(t)dt + vo(0)
in cui vo(0) può essere reso nullo e quindi, a parte il segno ed il fattore 1RC, il valore vo(T) corrisponde a quello che si trova allo stesso istante in uscita da un filtro adattato [402]   [402] Il circuito non lineare mostrato non è un filtro adattato, dato che per t > T non produce la stessa uscita (vedi http://dsp.stackexchange.com/questions/9094/understanding-matched-filter). alla g(t) rettangolare. L’interruttore che scarica (dump) la capacità C per t = nT ha lo scopo di azzerare la vo(0) prima della ricezione di un successivo impulso, rendendo possibile l’uso dello schema per la detezione ottima di flussi binari a velocità fb = 1⁄T.
Rumore colorato
Nel caso in cui PN(f) non sia pari ad una costante, la condizione per massimizzare (10.174) non è più la (10.172), bensì deve risultare [403]   [403] La condizione (10.175) si ottiene anche in questo caso imponendo la massimizzazione di SNR = (mH1z(T))2⁄σ2z(T) = | ∫∞−∞Hr(f)G(f) e j2πfTdf|2 ∫∞−∞|HR(f)|2 PN(f)df il cui denominatore tiene conto che σ2z(T) = ∫∞−∞PZ(f)df è dovuta al solo rumore. Applichiamo ora a SNR la diseguaglianza di Schwartz posta nella forma
|∞⌠⌡ −∞a(θ)b*(θ)dθ|2∞⌠⌡ −∞|a(θ)|2dθ  ≤ ∞⌠⌡ −∞|b(θ)|2dθ
e identifichiamo a(θ) con HR(f)√PN(f) e b*(θ) con G(f) e j2πfT⁄√ PN(f) . Imponendo di nuovo la condizione a(θ) = k ⋅ b(θ) con k = 1, otteniamo il massimo SNR come SNR = ∫∞−∞|b(θ)|2dθ = ∫∞−∞|G(f)|2  PN(f) df, e quindi scrivendo a(θ) = b(θ) ossia HR(f)√PN(f)  = G*(f)e −j2πfT⁄√ PN(f) si ottiene il risultato (10.175).
(10.175) HR(f) = G*(f) e −j2πfT PN(f)
in modo che HR(f), oltre ad esaltare le frequenze per le quali lo spettro del segnale è maggiore, riesce anche ad attenuare quelle per le quali la potenza di rumore è più grande. Riscrivendo la (10.175) come
HR(f) = 1√  PN(f) G*(f) √PN(f) e −j2πfT = Hw(f)Ha(f)
si può giungere alla interessante interpretazione illustrata in figura: il segnale ricevuto, in cui è presente sia il segnale g(t) che il rumore colorato υ(t), attraversa innanzitutto
figure fadatt-rumcol.png
un filtro sbiancante [404]   [404] Detto whitening filter in inglese. con risposta in frequenza Hw(f) = 1√  PN(f) e risposta impulsiva hw(t), così chiamato perché ha lo scopo di rendere il rumore bianco. Quindi, viene attraversato il filtro adattato all’impulso sbiancato, ossia alla forma d’onda gw(t) = g(t) * hw(t) con trasformata Gw(f) = G(f) √PN(f) , risultato del transito di g(t) attraverso Hw(f).
Assenza di rumore
Qualora non sia presente rumore, l’andamento dell’uscita del filtro adattato è proprio pari (a meno del ritardo T) alla funzione di autocorrelazione di g(t), che viene campionata in corrispondenza del suo massimo.
Probabilità di errore
Tornando al caso di rumore bianco, in base al ragionamento esposto alla nota 392 nel caso di equiprobabilità delle due ipotesi H1 e H0, la Pe è pari alla probabilità che una v.a. gaussiana con media nulla e varianza σ2 =  N0 2 EG sia maggiore di EG2; tale valore può essere calcolato applicando l’eq. (10.121) a pag. 1, in modo da ottenere
Pe =  1 2  erfc⎧⎨⎩EG⁄2√ 2 √N0 2 EG ⎫⎬⎭ = 1 2  erfc⎧⎨⎩1 2 √ EG N0 ⎫⎬⎭
Esempio con i dati riportati nell’esempio di pag.1, per la probabilità di errore nel caso di H0 e H1 equiprobabili si ottiene
Pe =  1 2  erfc⎧⎨⎩1 2 √ EG N0 ⎫⎬⎭ = 1 2  erfc⎧⎨⎩1 2 √ 4 ⋅ 10− 1 10− 1 ⎫⎬⎭ = 1 2  erfc{1} ≃ 1.5 ⋅ 10− 1
(si utilizzi la fig. 6.9 a pag. 1).
Ma questa non è la minima Pe conseguibile, che si ottiene invece nel caso di segnalazione antipodale, molto più indicata nel caso in cui lo scopo del ricevitore non sia di individuare un solo impulso isolato, ma una sequenza simbolica binaria.

7.6.1 Segnalazione antipodale

Volendo distinguere tra due possibili messaggi (ad es, x1 ed x2), la scelta ottima per rendere minima la probabilità di errore consiste nell’adottare x1(t) = g(t), x2(t) = − x1(t), e di porre in ingresso al ricevitore un filtro adattato a g(t).
In questo modo l’uscita del filtro all’istante di campionamento rappresenta una v.a. gaussiana z con media mz = ±EG (a seconda se sia stato trasmesso x1 o x2) e varianza σ2z =  N0 2 EG.
figure f7.157a.png
Pertanto ora la soglia di decisione è pari a zero, e nel caso di simboli equiprobabili, in base alla nota 392, la probabilità di errore Pe corrisponde a quella di eccedere EG per una v.a. gaussiana a media nulla: in conseguenza del risultato (10.121) di pag. 1 si ottiene quindi
(10.176)
Pe = 1 2  erfc⎧⎨⎩EG √2√N0 2 EG ⎫⎬⎭ = 1 2  erfc⎧⎨⎩√EGN0 ⎫⎬⎭
che, come vedremo all’eq. (21.18), rappresentano anche le prestazioni ottenibili per un segnale dati binario a banda minima.

7.6.2 Segnalazione ortogonale

Dovendo trasmettere N diversi messaggi (x1, x2,  ..., xN), possiamo associare ad ognuno di essi una forma d’onda xi(t) tale che ∫xi(t)xj(t)dt = 0 con i ≠ j, ovvero in modo che i segnali xi(t) siano ortogonali. In tal caso il ricevitore ottimo è costituito da un banco di filtri, ognuno adattato ad una diversa xi(t), in modo che, in assenza di rumore, la ricezione di una delle forme d’onda xi(t) non produca nessuna uscita sui filtri del banco per j ≠ i. In presenza di rumore, la decisione su cosa sia stato trasmesso viene presa valutando quale dei filtri presenti il valore massimo in corrispondenza dell’istante di campionamento, realizzando così un ricevitore a correlazione (vedi § 16.5 a pag. 1).
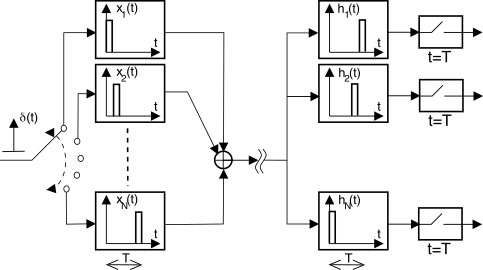
Esempio L’impulso δ(t) entra in uno di filtri mostrati nella figura 7.20 , le cui risposte impulsive xi(t) realizzano una famiglia di funzioni ortogonali, dato che le rispettive forme d’onda non si sovrappongono nel tempo. In ricezione, solo uno dei filtri adattati con risposta impulsiva hi(t) produce una uscita diversa da zero per t = T,  come verificabile ricordando la costruzione grafica dell’operazione di convoluzione mostrata a pag. 1.
figure f7.158.png
Figure 7.20 Schema di ricevitore a correlazione
Multiplazione a divisione di codice
La trasmissione mediante forme d’onda ortogonali può essere applicata alla tecnica di accesso multiplo a divisione di codice o cdma [405]   [405] (vedi § 11.1.1.3, § 16.9.2.5), qualora ogni utente usi una forma d’onda ortogonale a quella degli altri, ed il ricevitore usi un filtro adattato programmabile in modo da discriminare uno solo tra tutti i codici ricevuti contemporaneamente.
Correlatore
figure f7.159.png
Si tratta di un modo alternativo di realizzare un filtro adattato, derivante dall’osservazione che il suo ruolo essenzialmente si riduce al calcolo della intercorrelazione (eq. (10.156)) tra il segnale ricevuto e quello atteso. Tale funzione può essere realizzata anche ricorrendo allo schema in figura, dove un integratore (implementato ad es. mediante il circuito integrate and dump, pag. 1) opera sul prodotto tra il segnale in arrivo ed una copia locale del coniugato [406]   [406] Anche se nel caso di banda base il segnale trasmesso è reale, volendo applicare la teoria esposta ad un inviluppo complesso (§ 11.2.1) si rende necessario tener conto dell’operazione di coniugato. della forma d’onda trasmessa. Un caso di applicazione di questo schema si trova al § 16.5.1 a proposito del ricevitore fsk ortogonale, mentre una variante idonea a stimare l’autocorrelazione di y(t) è proposta al § 7.5.4.
 Sezione 7.5: Operazioni elementari sui segnali Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.7: Appendici