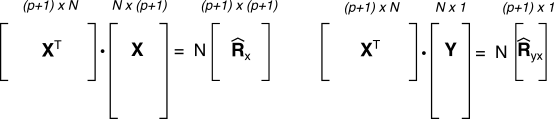7.7 Appendici
Un capitolo così ad ampio respiro non può che ospitare una serie di appendici altrettanto variate!
7.7.1 Regressione lineare
Riprendiamo il modello accennato a pag.
1 per approfondire il metodo di predizione del valore atteso di una v.a.
y a partire dalla conoscenza di una una seconda v.a.
x (il
regressore) correlata alla prima, in base alla relazione
in cui
ε rappresenta un errore additivo anch’esso aleatorio, a media nulla e statisticamente indipendente sia da
x che da
y. Per determinare il valore dei parametri del modello
a e
b, si imposta un problema di minimizzazione a carico della varianza dell’errore
σ2ε = E{(y − ax − b)2} risolvibile eguagliando a zero le derivate di
σ2ε rispetto ad
a e
b. ovvero
Dalla seconda delle
(10.178) otteniamo
b = my − amx che sostituito nella prima dopo pochi passaggi permette di ottenere
a [m(2)x − (mx)2] = mxy − mxmy. Sostituendo ora
[m(2)x − (mx)2] con
σ2x (vedi eq.
(10.119)), e
mxy − mxmy con
σxy (eq.
(10.152)), si ottiene per
a l’espressione riportata sotto, che a sua volta sostituita nella seconda delle
(10.178)
produce
che sono i valori da utilizzare nella
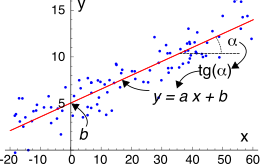
retta di regressione y = ax + b esemplificata nella figura a lato
assieme ad una
nuvola (o meglio
set) di coppie
(xi, yi) di misurazioni sperimentali, che vengono utilizzate per effettuare una
stima campionaria (vedi §
6.6.3.1)
m̂x = 1N ∑Ni = 1xi, m̂y = 1N ∑Ni = 1yi, m̂(2)x = 1N ∑Ni = 1x2i e m̂x, y = 1N ∑Ni = 1xiyi
delle correlazioni che compaiono in
(10.179).
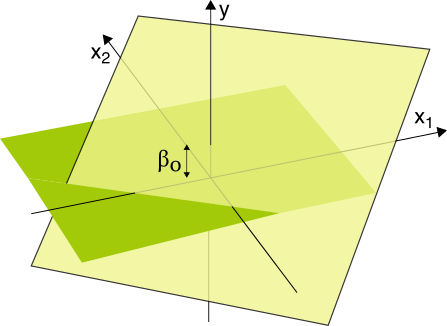
Costituisce una versione
vettoriale del precedente problema esteso al caso in cui i regressori siano più di uno, ovvero qualora al posto della
(10.177) si
supponga una relazione del tipo
in modo che per
p = 2 la retta di regressione divenga
un piano con
β0 pari all’intercetta sull’asse delle quote
y quando i regressori
x sono nulli, mentre per
p > 2 si ha un
iperpiano.
L’individuazione dei coefficienti
β = (β0, β1, ⋯, βp) (detti ora
predittori) viene nuovamente affidato al criterio di minimizzare il valore quadratico atteso della grandezza di errore, ovvero cercando
in cui
avendo aggiunto un regressore
fittizio x0 = 1, ovvero adottato un vettore
aumentato di regressori
x = (1, x1, x2, ⋯, xp).
Azzerando le derivate parziali di
(10.182) rispetto ai predittori
βk si ottiene il sistema di
p + 1 equazioni in
p + 1 incognite simile a quello di §
18.4.2:
in cui
Rx è la matrice
simmetrica (p + 1) × (p + 1) delle correlazioni tra i regressori
xh ed
xk con elementi
rhk = rkh = m(1, 1)xhxk ed
Ryx è il vettore delle intercorrelazioni tra i regressori ed il valore
y, con elementi
ryxh = m(1, 1)yxh.
Prima di continuare formalizziamo la notazione con cui descrivere i dati da utilizzare nella stima delle correlazioni
Rx e
Ryx. Pensiamo cioè di collezionare
N coppie
(yi, xi) con
N ≫ p, in cui
yi è la variabile di osservazione ed xi è il vettore (1, xi1, xi2, ⋯, xip) dei regressori osservati congiuntamente, e di allineare i vettori
xi in altrettante righe di una matrice X di formato N × (p + 1), in modo da poter scrivere la (10.180) (priva del termine di errore ε) nella forma di un sistema
di N equazioni nelle p + 1 incognite β0, β1, ⋯, βp. Con questa notazione, le stime R̂x e R̂yx degli elementi che compaiono nella (10.183) possono essere espresse come
In modo da ottenere un valore per β* ottimo pari a
Metodo dei minimi quadrati
Affronta la stima dei predittori
β adottando il criterio di minimizzare la norma quadratica
∥ε∥2 = ∥ y − X ⋅ β∥2 della differenza tra i due membri di
(10.184), ovvero tra il vettore delle osservazioni
y e quello delle relative predizioni sulla base dei regressori. In questo caso scriviamo pertanto
Questa espressione si presta ad una interessante interpretazione geometrica, che consente di arrivare in modo agevole allo stesso risultato già trovato
(10.186).
Errore ortogonale alla predizione
Indicando con
ŷ = X ⋅ β* il vettore ottenuto applicando il risultato
(10.187) alla relazione
(10.184), osserviamo che
ŷ è vincolato a giacere nell’iper-piano
X generato dalle (sole)
(p + 1) colonne
ξh di
X, combinate linearmente
dai predittori
β*, potendo scrivere
mentre
y può variare in uno spazio di dimensione
N ≫ p. Dunque scrivere
significa che il vettore di errore
ε spiega ciò che non può essere descritto da una combinazione lineare delle colonne
ξh, ovvero ha
proiezione nulla in
X, ossia giace in uno spazio
ortogonale ad
X in cui è costretto a stare
ŷ. Come conseguenza si ottiene che
ε è ortogonale a
tutte le colonne
ξh ovvero possiamo scrivere
X⊤ ⋅ ε = 0, il che ci viene comodo perché se premoltiplichiamo ambo i membri di
per
X⊤ si ottiene
X⊤y = X⊤X ⋅ β* + X⊤ε = X⊤X ⋅ β* e dunque
in cui
X+ = (X⊤X)− 1 X⊤ prende il nome di
pseudoinversa in quanto pur
non essendo
X quadrata e dunque invertibile, oltre ad essere il sistema
(10.184) sovradeterminato avendo più equazioni che incognite, permette di giungere comunque ad una soluzione a
minima distanza (10.187).
Mostriamo ora che il valore di
β* ottenuto con la
(10.188) in base al criterio
(10.187) è esattamente lo stesso di quello ottenuto dalla
(10.186) con il criterio
(10.181). A tal fine notiamo che le
(10.186) e
(10.188) sono equivalenti tra loro, in quanto l’applicazione delle regole del prodotto tra matrici porta alle stesse espressioni
(10.185), a meno di un fattore
N che poi si elide, potendo dunque scrivere
R̂x = 1N X⊤X e R̂yx = 1N X⊤y
come anche illustrato alla figura seguente.
7.7.2 Coefficiente di correlazione di Pearson
I diagrammi di esempio presentati alla fig.
7.3 basano la valutazione di quanto una coppia di v.a.
x ed
y siano correlate anche sul calcolo del
coefficiente di correlazione ρxy, che ha valori compresi tra
+ 1 e
− 1, ed è definito come
ρxy = σxy σxσy
In tal modo, si opera una normalizzazione del valore della covarianza
σxy, rispetto alle deviazioni standard
σx e
σy delle due v.a., rendendo così il valore di
ρ indipendente dalla dinamica dei valori assunti da
x ed
y.
Anche il coefficiente
ρ si presta ad una interessante interpretazione geometrica, una volta messe in relazione la deviazione standard
σx con la norma
∥x∥ di
x (vedi §
2.4), e la covarianza
σxy con il prodotto scalare
⟨x, y⟩ tra
x ed
y. In tale contesto possiamo definire due v.a. come
ortogonali se risulta
σxy = ρxy = 0, mentre un valore
ρxy = ±1 indica che una delle due v.a. è sempre proporzionale all’altra, con un fattore costante. Ricordiamo che l’ortogonalità
ρxy = 0 esprime unicamente l’assenza di legami di tipo
lineare tra
x ed
y, come esemplificato dal caso
di fig. 7.3. Citiamo inoltre l’estensione formale del risultato noto come
disuguaglianza di Schwartz (pag.
1), una volta che al coefficiente di correlazione
ρxy sia stato associato il concetto di coseno tra
x ed
y: una tale identificazione deriva dall’essere
− 1 < ρxy < 1, e permette di asserire che
|σxy| ≤ σxσy.
7.7.3 Teorema di Wiener per processi
Sviluppiamo qui la dimostrazione che
Px(f) = F {Rx(τ)} anche se
x(t) rappresenta un generico membro di un processo, nelle condizioni espresse alla nota
365. Considerando un segmento
xT(t) = x(t)rectT(t) di durata
T estratto da un membro del processo, iniziamo dalla definizione (§
7.3.1)
Px(f) = limT → ∞ 1T E{|XT(f)|2} in cui
XT(f) = F {xT(t)}, e dunque
dove riconosciamo
E{x*(t1)x(t2)} essere pari al momento misto
(10.150), che indichiamo per uniformità come
Rx(t1, t2) ovvero come
Rx(t, t + τ) dopo aver posto l’istante
t1 pari ad un generico valore
t, ed aver espresso
t2 come
t2 = t + τ. Con la nuova notazione, l’espressione
(10.189) diviene
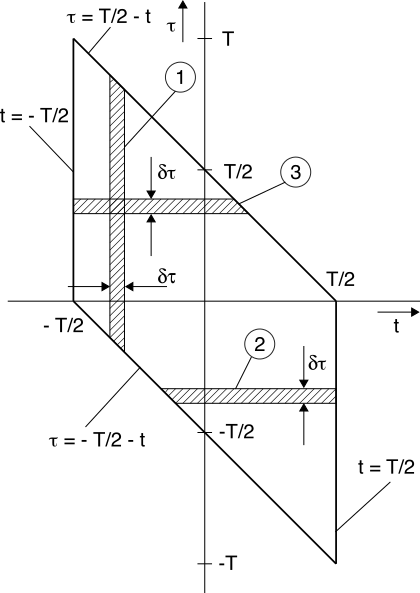
∫t = T⁄2t = − T⁄2 ∫τ = T⁄2 − tτ = − T⁄2 − tRx(t, t + τ)e −j2πfτdτdt ➀
Teniamo ora in considerazione il dominio di integrazione mostrato a lato, dove l’area ➀ rappresenta quella dell’integrale interno, per il differenziale
dt: se scambiamo l’ordine di integrazione, suddividendo l’integrale su
τ in due parti, per le quali
τ < 0 e
τ > 0, e corrispondenti alle aree ➁ e ➂ in figura, otteniamo
∫0 − T ⎡⎣ ∫t = T⁄2t = − T⁄2 − τRx(t, t + τ)e −j2πfτdt⎤⎦dτ ➁ + ∫T0 ⎡⎣ ∫t = T⁄2 − τt = − T⁄2Rx(t, t + τ)e −j2πfτdt⎤⎦dτ ➂
Considerando ora il processo stazionario, scriviamo
Rx(t, t + τ) = Rx(τ), che portiamo fuori dall’integrale su
t:
E{|XT(f)|2} = 0⌠⌡ − T⎡⎢⎣T⁄2⌠⌡ − T⁄2 − τdt⎤⎥⎦Rx(τ)e −j2πfτdτ + T⌠⌡0⎡⎢⎣T⁄2 − τ⌠⌡ − T⁄2dt⎤⎥⎦Rx(τ)e −j2πfτdτ = = 0⌠⌡ − T(T + τ)Rx(τ)e −j2πfτdτ + T⌠⌡0(T − τ)Rx(τ)e −j2πfτdτ = = T⌠⌡ − T(T − |τ|)Rx(τ)e −j2πfτdτ
dato che per
τ < 0 risulta
τ = − |τ|. Sostituiamo l’ultimo risultato nell’espressione
Px(f) = limT → ∞ 1TE{|XT(f)|2}, ottenendo
Px(f) = limT → ∞ T⌠⌡ − TT − |τ| T Rx(τ) e −j2πfτ dτ = = ∞⌠⌡ − ∞Rx(τ) e −j2πfτ dτ − limT → ∞ T⌠⌡ − T|τ|T Rx(τ) e −j2πfτ dτ
in cui il secondo termine si annulla se
∫∞−∞|τRx(τ)|dτ < ∞, e ciò dimostra il teorema discusso al §
7.2.1.
7.7.4 Densità spettrale per onda PAM
L’acronimo
pam sta per
Pulse Amplitude Modulation (pag.
1), e individua una classe di segnali realizzati ripetendo indefinitivamente uno stesso im
pulso elementare
g(t) con periodo
T, ognuno moltiplicato (o
modulato in ampiezza) per un diverso coefficiente
an. Sebbene in questa definizione possa rientrare anche il caso in cui gli
an siano campioni di un segnale analogico (§
4.1), focalizziamo la trattazione al caso in cui rappresentino invece
i simboli di una trasmissione numerica con periodo di simbolo
T, a valori reali nel caso di banda base (§
15.1.2), o complessi nel caso di una modulazione numerica, mentre
g(t) rappresenta un
impulso dati, del tipo a banda infinita (§
15.2.1) oppure di Nyquist (§
15.2.2.2).
Scriviamo pertanto l’onda
pam nella forma
in cui
θ è una v.a. uniformemente distribuita tra
± T 2 in modo che la
(10.190) rappresenti un membro di un processo stazionario ergodico (vedi pag.
1), e verifichiamo il risultato
semplice riportato al §
7.2.5, ossia che nel caso in cui i valori discreti
an siano realizzazioni di v.a. statisticamente indipendenti, a media nulla, identicamente distribuite e con varianza
σ2A = E{a2n}, il segnale dati è a media nulla, e ad esso corrisponde uno spettro di densità di potenza
pari a
Allo scopo di arrivare ad un risultato più generale, sviluppiamo i calcoli rimuovendo le ipotesi restrittive di indipendenza statistica e media nulla per gli
an, per poi riapplicarle una alla volta.
Essendo
x(t) membro di un processo ergodico, il valor medio di una sua realizzazione può essere calcolato come valore atteso rispetto alle fonti di aleatorietà, ossia i simboli
an ed il ritardo
θ
mX = EA, Θ{∞⎲⎳n = −∞ang(t − nT − θ)} = ∞⎲⎳n = −∞EA{an}EΘ{g(t − nT − θ)}
avendo assunto l’indipendenza statistica tra
A e
Θ. Ponendo
EA{an} = mA, sviluppando il valore atteso di
g(.), e ricordando che
pΘ(θ) = 1 T rectT(θ), otteniamo
mX = mA ∞⎲⎳n = −∞∞⌠⌡ −∞g(t − nT − θ)pΘ(θ)dθ = = mA T ∞⎲⎳n = −∞T⁄2⌠⌡ − T⁄2g(t − nT − θ)dθ = mA T ∞⎲⎳n = −∞t − nT + T⁄2⌠⌡t − nT − T⁄2g(u)du = = mA T ∞⌠⌡ −∞g(u)du = mA T G(0)
avendo posto al terzo passaggio
u = t − nT − θ, ad avendo notato al penultimo che gli estremi di integrazione entro la sommatoria sono contigui ed abbracciano tutto il dominio di integrazione. Una prima osservazione che traiamo è che anche se la sequenza degli
an non fosse a media nulla, è possibile ottenere
mX = 0 adottando una
g(t) ad area nulla, come ad esempio per un codice Manchester o differenziale (pag.
1), o per le forme d’onda adottate nell’
fsk ortogonale incoerente (§
16.12.1).
Spettro di densità di potenza
In accordo al teorema di Wiener (§
7.2.1), procediamo con il calcolo del momento misto
RX(τ) = E{x(t)x(t + τ)} e quindi ne effettuiamo la trasformata di Fourier. Anche qui l’indipendenza statistica tra
Θ ed
A permette di scrivere
RX(τ) = ∞⎲⎳n = −∞∞⎲⎳m = −∞E{anam}E{g(t − nT − θ)g(t + τ − mT − θ)} = = ∞⎲⎳n = −∞∞⎲⎳m = −∞RA(m − n) 1 T T⁄2⌠⌡ − T⁄2g(t − nT − θ)g(t + τ − mT − θ)dθ = = 1 T ∞⎲⎳n = −∞∞⎲⎳k = −∞RA(k) T⁄2⌠⌡ − T⁄2g(t − nT − θ)g(t + τ − (k + n)T − θ)dθ = = 1 T ∞⎲⎳k = −∞RA(k) ∞⎲⎳n = −∞t − nT + T⁄2⌠⌡t − nT − T⁄2g(u)g(u + τ − kT)du = = 1 T ∞⎲⎳k = −∞RA(k) ∞⌠⌡ −∞g(u)g(u + τ − kT)du = 1T ∞⎲⎳k = −∞RA(k)RG(τ − kT)
in cui al secondo passaggio si è sfruttata la stazionarietà della sequenza
an per cui
E{anam} = RA(m − n), al terzo si è posto
k = m − n, al quarto si è posto
u = t − nT − θ, al penultimo si sono riuniti gli infiniti integrali su domini contigui in uno solo, ed all’ultimo si è riconosciuto l’integrale come quello che definisce l’autocorrelazione (traslata) di
g(t), indicata come
RG(τ − kT). La trasformata di Fourier del risultato finale produce
in cui
|G(f)|2 = F {RG(τ)} è lo spettro di densità di energia dell’impulso
g(t), ed il termine
e −j2πfkT consegue dalla traslazione temporale di
RG(τ). L’espressione
rappresenta la
dtft (§
4.4) di
RA(k) e prende il nome di
spettro del codice, mostrando come le caratteristiche statistiche degli
an contribuiscano a determinare la densità spettrale per il segnale dati associato.
Iniziamo a semplificare il risultato
(10.192) considerando il caso in cui i simboli
an siano statisticamente indipendenti, ma a media non nulla. In questo caso si ottiene
RA(k) = ⎧⎨⎩ m2A + σ2A k = 0 m2A k ≠ 0
e quindi la
(10.193) diviene
avendo sfruttato il risultato
(10.61) a pag.
1 relativo alla trasformata di un treno di impulsi . Sostituendo ora la
(10.194) nella
(10.193) e quindi in
(10.192), per quest’ultima si ottiene
che evidenzia la presenza nello spettro di una componente
continua, assieme ad una componente
a righe sulle frequenze armoniche di quella di simbolo
fs = 1T, descritta agli impulsi di area
m2A T2 |G(f)|2; scegliendo dunque un impulso dati tale che
G(f) si annulli per
f = k T, tali righe possono essere eliminate. E’ per questo motivo che (ad es.) la segnalazione di tipo
rz (vedi §
15.2.1) presenta la componente ad
f = fs, vedi l’esercizio seguente.
Simboli a valor medio nullo
Nel caso in cui la sequenza
an oltre ad essere incorrelata presenti anche un valor medio nullo, ovvero
mA = 0, la
(10.195) si semplifica ulteriormente e fornisce il risultato
semplice già noto:
PX(f) = σ2A T |G(f)|2
Esempio Applichiamo i risultati a cui siamo pervenuti ai
codici di linea discussi al §
15.2.1, come ad esempio il codice
rz, che adotta un impulso
g(t) = Arectτ(t) con
τ < T, per il quale risulta
|G(f)|2 = (Aτ)2 sinc2(fτ). Se i simboli trasmessi
an sono equiprobabili, incorrelati, ed a valori binari
0 od
1, si ottiene che
mA = E{a} = 1⁄2 ⋅ 1 + 1⁄2 ⋅ 0 = 1⁄2 σ2A = E{(a − mA)2} = 1⁄2 ⋅ 1⁄4 + 1⁄2 ⋅ 1⁄4 = 1⁄4
Pertanto la
(10.195) fornisce
PRZ(f) = (Aτ)2 sinc2(fτ) T ⎡⎢⎣14 + 14 1T ∞⎲⎳k = −∞δ(f − k T)⎤⎥⎦
Nel caso in cui risulti
τ = T⁄2, la sommatoria presenta termini non nulli per i soli indici dispari, con area degli impulsi pari a
sinc2(k⁄2) = (2⁄kπ)2, dunque si ottiene
PRZ(f) = A2T 16⎛⎜⎝ sinc2⎛⎝fT 2⎞⎠ + 1T ∞⎲⎳k dispari = −∞⎛⎝2kπ⎞⎠2δ⎛⎝f − k T⎞⎠⎞⎟⎠
che presenta impulsi per
f = 1⁄T, 3⁄T, 5⁄T.... Il risultato ottenuto è mostrato in fig.
7.26, in cui si è adottata una scala delle frequenze normalizzata, mentre per le ampiezze si è scelta una rappresentazione in dB (§
8.1) allo scopo di evidenziare come, all’aumentare della frequenza di simbolo
fs = 1⁄T, la componente a righe tende a
prevalere rispetto a quella continua, dato che al diminuire di
T la durata di
g(t) è sempre minore, e così la sua energia. Notiamo inoltre che essendo i simboli
equiprobabili, si può ottenere
mA = 0 e la conseguente scomparsa delle righe spettrali semplicemente scegliendo i valori degli
an come
+ 1 (ad esempio per l’uno) e
− 1 (per lo zero), ovvero adottando una segnalazione
antipodale (§
7.6.1).
-
Facendo tendere τ → T, l’impulso si trasforma in nrz, per il quale |G(f)|2 = (AT)2 sinc2(fT), che si azzera esattamente ai multipli della frequenza di simbolo in cui sono centrati gli impulsi, annullando quindi tutti i termini della sommatoria, indipendentemente dalla scelta degli an, e dando luogo al risultato PNRZ(f) = A2T 4 sinc2(fT), in accordo alla (10.191).
7.7.5 Autocorrelazione di un processo in uscita da un filtro
Al §
204 si è affermato che, quando un processo stazionario almeno in senso lato attraversa un filtro, il processo di uscita è caratterizzato da una autocorrelazione
Ry(τ) = Rx(τ) * Rh(τ). Mostriamo che è vero.
dato che
∫h(β)Rx(τ + α − β)dβ che compare nella
(10.196) è pari alla convoluzione tra
h(t) e
Rx(t) calcolata per
t = τ + α, ovvero
∫h(β)Rx(τ + α − β)dβ = Rx(t) * h(t)|t = τ + α
che (vedi l’eq.
(10.157) a pag.
1) a sua volta può essere espressa come
dove all’ultimo passaggio si è applicata la definizione della intercorrelazione
(10.156), oltre che la
(10.157), ottenendo così la
(10.196).
Per arrivare al risultato desiderato, osserviamo ora che applicando la
(10.198) alla
(10.196), quest’ultima può essere riscritta come
Ry(τ) = Rxy(τ) * h(−τ) = Rx(τ) * h(τ) * h(−τ)
che, una volta
F -trasformata, equivale a
Osserviamo infine che se il processo di ingresso oltre ad essere stazionario è anche ergodico, l’antitrasformata della
(10.199) si riscrive come
m(1, 1)y = m(1, 1)x * Rh(τ).
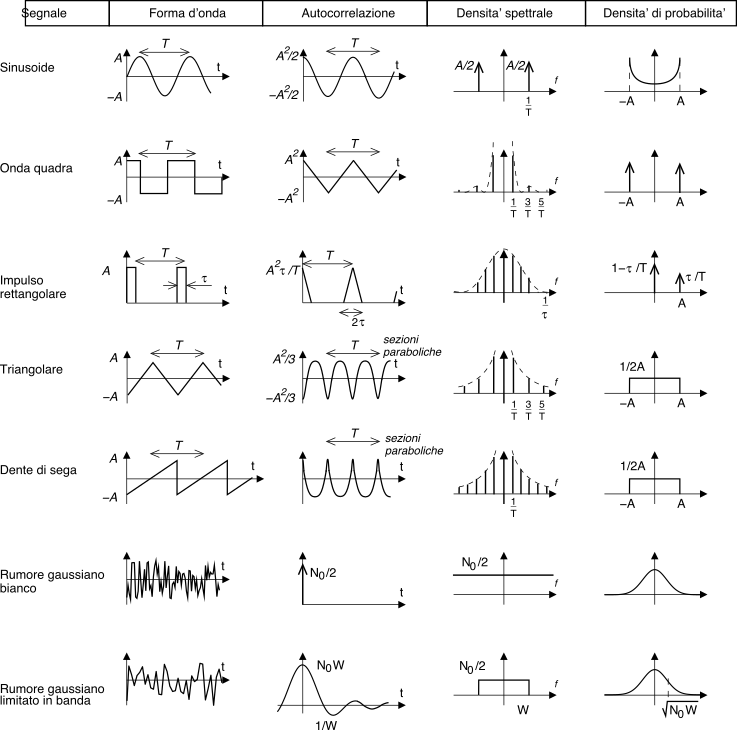
7.7.6 Grafici di esempio
Di seguito sono riportati i grafici della forma d’onda, dell’autocorrelazione, della densità spettrale e della densità di probabilità, per alcuni segnali tipici.