3.6 Derivazione ed integrazione nel tempo
Queste due proprietà sono di applicazione meno frequente, ma talvolta utile. In particolare, si verifica che le operazioni di derivata ed integrale di un segnale possono essere realizzate mediante il passaggio dello stesso attraverso un filtro, dato che derivata ed integrale nel tempo sono equivalenti a prodotti in frequenza, e quindi realizzabili come convoluzione del segnale con una appropriata risposta impulsiva.
La trasformata
Y(f) di un segnale
y(t) = ddtx(t) è esprimibile in funzione della trasformata di
x(t) come
e più in generale si ha
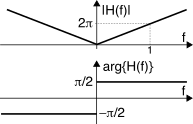
F {dndtn x(t)} = (j2πf)n ⋅ X(f). L’andamento del modulo dello spettro originario
|X(f)| risulta pertanto
esaltato alle frequenze più elevate, con legge proporzionale ad
f, come risulta dal prodotto per
2π|f|. Osservando poi che il numero
immaginario puro j2πf = 2πf e jπ2sgn(f) ha fase
± π2 con segno uguale a quello di
f,
troviamo che la fase di
X(f) subisce un incremento di
π2 per frequenze positive, ed un eguale decremento per quelle negative. Pertanto, la derivata di un segnale corrisponde all’uscita di un filtro descritto dalla risposta in frequenza riportata a lato.
Esercizio Calcolare Y(f) = F {y(t)}, considerando y(t) = ddt x(t) e x(t) = cos2πf1t + cos2πf2t. Valutare poi y(t) = F −1{Y(f)} nel caso in cui f1 = 10 e f2 = 100 Hz.
-
Anziché applicare le regole di derivazione e quindi effettuare la trasformata, scegliamo di calcolare prima X(f), e quindi applicare la (10.54) :
X(f) = 1⁄2[δ(f − f1) + δ(f + f1) + δ(f − f2) + δ(f + f2)]
Dato che (pag. 1 ) f ⋅ δ(f±a) = ∓a ⋅ δ(f±a), il prodotto Y(f) = j2πf ⋅ X(f) fornisce
Y(f) = j2π2{f1[δ(f − f1) − δ(f + f1)] + f2[δ(f − f2) − δ(f + f2)]}
Considerando infine che j2π2 = − 2π2j, si ottiene y(t) = − 2πf1sin2πf1t − 2πf2sin2πf2t e quindi, per f1 = 10 e f2 = 100, si ha
y(t) = − 2π[10sinω1t + 100sinω2t]
Il doppietto Viene da chiedersi quale sia la risposta impulsiva
h(t) di un filtro derivatore. Dato che per definizione
h(t) rappresenta l’uscita corrispondente ad un ingresso impulsivo
δ(t), evidentemente deve risultare
h(t) = δ’(t), ovvero pari alla derivata dell’impulso. ok, ma come è fatto
δ’(t), e perché viene detto doppietto ? Per rispondere occorre fare un passo indietro, e tornare a pensare l’impulso come una distribuzione, ad es.
δ(t) = limτ → 0 1τ rectτ(t), e considerare che
ddt rectτ(t) = δ⎛⎝t + τ2⎞⎠ − δ⎛⎝t − τ2⎞⎠ , ossia due impulsi di segno opposto, centrati in corrispondenza delle discontinuità . Pertanto risulta
δ’(t) = limτ → 0 1τ ⎡⎣δ⎛⎝t + τ2⎞⎠ − δ⎛⎝t − τ2⎞⎠⎤⎦, ovvero due impulsi di area infinita e segno opposto, entrambi centrati in
t = 0.
Indicando il segnale integrale (o primitiva) come
y(t) = ∫t−∞x(θ)dθ, il legame tra integrale e derivata permette di scrivere
In analogia alla derivata, la
(10.55) rappresenta l’uscita di un filtro integratore con risposta in frequenza
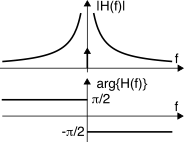
H(f) = − j12πf, che quindi
esalta le frequenze più basse del segnale originario in accordo all’andamento iperbolico di
|H(f)| = 1⁄2π|f|, mentre la fase
arg{H(f)} = − π2 sgn(f) subisce una alterazione
opposta al caso della derivata, dato che ora
j ha cambiato segno.
Notiamo però che il risultato
(10.55) manifesta la comparsa di una
singolarità in
f = 0 se
X(0) ≠ 0: come mostrato a pag.
1, ciò corrisponde ad un segnale
x(t) che sottende un’area non nulla, e quindi
y(t) = ∫t−∞x(θ)dθ non si azzera per
t → ∞. In questo caso
y(t) non è di energia, ed il calcolo della sua trasformata richiede qualche
espediente, che aggiunge ad
H(f) = − j12πf il termine
12 δ(f), anch’esso mostrato in figura.
Esercizio Trasformata di un triangolo.
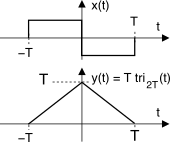
Consideriamo un segnale ad area nulla
x(t) =
rectT⎛⎝t +
T2⎞⎠ −
rectT⎛⎝t −
T2⎞⎠ ed il suo integrale
y(t) =
t⌠⌡ − ∞x(θ)dθ =
T tri2T(t) entrambi rappresentati in figura:
y(t) è nullo fino a
t < − T, cresce linearmente fino a
t = 0, e quindi il contributo all’integrale dato dall’area del
rect negativo torna ad annullarne il valore. Per calcolare la
F -trasformata di
y(t), calcoliamo prima quella di
x(t), e poi applichiamo la proprietà dell’integrazione. Applicando la proprietà di traslazione nel tempo, scriviamo
X(f) = T ⋅ sinc(fT) ⋅ e +j2πfT2 − T ⋅ sinc(fT) ⋅ e −j2πfT2 = = T ⋅ sin(πfT)πfT ⋅ 2j sinπfT = j2 T sin2(πfT)πfT
Essendo
x(t) ad area nulla, la trasformata del suo integrale si ottiene dividendo
X(f) per
j2πf, ovvero
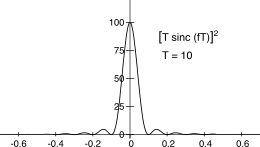
Y(f) = j2Tj2πf sin2(πfT)πfT TT = ⎛⎝T sin(πfT)πfT⎞⎠2 = (T sinc(fT))2
il cui andamento è mostrato in figura
3.18 . Da questo risultato consegue infine che
F {tri2T(t)} = T sinc2(fT), come riportato al §
3.8.8.
Densità di energia del rettangolo
Lo stesso risultato mostrato nell’esempio può essere ottenuto per altra via, notando che il triangolo è il risultato della convoluzione di due rettangoli:
Come verifica, si ripercorra la costruzione grafica riportata alla sezione
3.4.3. E’ quindi ora sufficiente applicare la proprietà del prodotto in frequenza, per ottenere:
Il risultato
(10.57) è anche pari alla densità di energia
Ez(f) di un segnale rettangolare
z(t) = rectT(t): infatti per il teorema di Parseval (eq.
(10.37)) si ha
Ez(f) = Z(f)Z*(f), in cui
Z(f) = F {rectT(t)} = Tsinc(fT), e pertanto
Prima di terminare il capitolo, definiamo un nuovo importante tipo di segnale tuttofare.