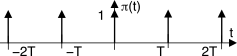
3.7 Treno di impulsi
La ripetizione periodica di un impulso di Dirac
δ(t) dà luogo ad un segnale del tutto particolare, il cui ruolo si rivelerà fondamentale in diversi aspetti trattati nel testo, come il campionamento (cap.
4) e la trasmissione numerica (cap.
15); nel seguito ne mostriamo una prima applicazione orientata ad ottenere la descrizione della trasformata per un segnale periodico, senza necessità di calcolare i relativi coefficienti di Fourier.
Un treno di impulsi (o segnale
a pettine) di periodo T viene rappresentato dal simbolo
πT(t) ed è realizzato come una serie infinita di impulsi di Dirac
Il segnale
πT(t) è periodico, e dunque può essere rappresentato mediante la relativa serie come
πT(t) = ∑∞n = −∞Πne j2πnFt con
F = 1T ed i cui coefficienti
Πn sono pari a
Πn = 1T T2⌠⌡ − T2[∞⎲⎳m = −∞δ(t − mT)] e −j2πnFtdt = = 1T T2⌠⌡ − T2δ(t) e −j2πnFtdt = 1T T2⌠⌡ − T21 ⋅ δ(t) dt = 1T
in quanto tra tutti gli impulsi della sommatoria ne resta solo uno, quello centrato in zero, dato che tutti gli altri cadono al di fuori dei limiti di integrazione, mentre la penultima eguaglianza tiene conto della
(10.43). Tutti i coefficienti risultano pertanto avere lo stesso valore, pari ad
1T, ottenendo lo sviluppo
Notiamo inoltre che, essendo
πT(t) un segnale reale pari, l’eq.
(10.60) può essere riscritta come una serie di coseni (vedi il §
2.2.1.3)
πT(t) = 1T + 2T ∑∞n = 1cos2πnFt.
Trasformata del treno di impulsi
Si può ottenere applicando la
(10.42) alla
(10.60) , ovvero
ottenendo così il risultato che la trasformata di un treno di impulsi è
a sua volta un treno di impulsi, di ampiezza
1⁄T, e con periodo (in frequenza) che è l’inverso di quello originario, cioè
F {πT(t)} = 1T Π1T(f).
Trasformata di un segnale periodico
Utilizziamo ora il risultato
(10.61) per ottenere una formula alternativa alla
(10.42) per un
generico segnale
x(t) periodico con periodo
T, che innanzitutto scriviamo come una serie infinita di ripetizioni di un suo periodo
g(t)
Sfruttando la proprietà
(10.49) di convoluzione con l’impulso traslato, la
(10.62) può essere scritta nei termini della
(10.59) come
x(t) =∞⎲⎳m = −∞g(t) * δ(t − mT) = g(t) *∞⎲⎳m = −∞δ(t − mT) = g(t) * πT(t)
dove nel secondo passaggio si è sfruttata la linearità della convoluzione. Ricordando ora la proprietà della moltiplicazione in frequenza
(10.52) otteniamo che lo spettro di
x(t) si esprime come
e quindi, sostituendo l’espressione di
F {πT(t)} ottenuta con la
(10.61) nella
(10.63) otteniamo
ovvero la trasformata di un segnale periodico
x(t) è pari al prodotto tra la trasformata
G(f) = F {g(t)} di un suo periodo, ed un treno di impulsi in frequenza di periodo
1T ed ampiezza
1T.
Esempio Riprendendo in considerazione il caso dell’onda quadra affrontato al §
2.2.1.4, non è difficile riconoscere come, ponendo
g(t) = A rectτ(t), a cui corrisponde
G(f) = A τ sinc(fτ), il prodotto di
G(f) per il treno di impulsi
1T ∑∞n = −∞δ(f − nF) (con
F = 1T) fornisce il risultato già incontrato:
X(f) = A τT ∞⎲⎳n = −∞ sinc(nFτ)δ(f − nF)
Il risultato ottenuto è un aspetto dell’uguaglianza nota come
somma di Poisson e che permette di esprimere un somma infinita basata su di una funzione nel tempo, nei termini di una somma infinita basata su di una funzione della frequenza, che è la trasformata di quella nel tempo. Nel caso in esame, antitrasformando entrambi i membri della
(10.64) si ottien
e
x(t) =∞⎲⎳m = −∞g(t − mT) =∞⎲⎳n = −∞1T G⎛⎝nT⎞⎠e j2πnTt
che riconosciamo corrispondere all’espansione in serie di Fourier del segnale periodico x(t), non appena constatato come i termini 1T G ⎛⎝nT⎞⎠ altro non sono che i suoi coefficienti Fourier, come d’altra parte risulta anche dalla (10.34).