Sezione 7.2: Spettro di densità di potenza Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.4: Filtraggio di segnali e processi  

7.3 Stima spettrale

Il teorema di Wiener (§ 7.2.1) ci aiuta qualora si desideri conoscere la densità di potenza per un processo ergodico, e se ne conosca l’autocorrelazione m(1, 1)X(τ) = RX(τ). Ma si ha spessoa che fare con processi di cui, pur ricorrendo le ipotesi di ergodicità, si ignorano le statistiche di insieme: un approccio può allora essere quello di stimare RX(τ) a partire dalle realizzazioni, come mostrato al § 7.5.4, e da quella ottenere Px(f). Un diverso caso tipico è quello di un segnale che, seppur rappresentativo di molti altri, presenta caratteristiche spettrali variabili nel tempo, e sono proprio queste variazioni a convogliare informazione [370]   [370] Un esempio può essere un segnale sonoro, ad esempio una voce recitante, per il quale vogliamo studiare le caratteristiche spettrali dei diversi suoni della lingua (i fonemi), per confrontarle con quelle di un altro individuo, o per ridurre la quantità di dati necessaria a trasmettere il segnale in forma numerica (vedi § 10.1.2), o per realizzare un dispositivo di riconoscimento vocale.. In tal caso conviene allora stimare direttamente Px(f) senza passare dall’autocorrelazione, a partire da un segmento temporale del segnale. Esistono al riguardo tecniche differenti, come ad es. quella riportata al § 10.1.2; per ora ci limitiamo ad un caso semplice ma di rilievo teorico.

7.3.1 Periodogramma

Data una realizzazione x(t, θi) di un processo, individuiamo un intervallo temporale T su cui definire un segnale a durata limitata xT(t) = x(t, θi)rectT(t). Questo segnale è di energia, con trasformata XT(f) e densità di energia ExT(f) = |XT(f)|2, e sotto le ipotesi di stazionarietà, da questo si può ottenere una stima ^Px(f) della densità di potenza Px(f) dell’intero segnale, semplicemente dividendo ExT(f) per la durata del segmento, ovvero
(10.165) ^Px(f) = PxT(f) = |XT(f)|2T
ottenendo una funzione della frequenza indicata come periodogramma, nome legato all’uso che ne fu inizialmente fatto, per scoprire tracce di periodicità in un segnale rumoroso. Al tendere di T ad ∞, la (10.165) tende alla vera densità di potenza limT → ∞ |XT(f)|2T = Px(f) della realizzazione xT(t, θi) e, se questa appartiene ad un processo ergodico [371]   [371] Nel caso contrario in cui x(t, θ) non sia ergodico, la sua densità spettrale può essere definita come Px(f) = limT → ∞ E{|XT(f)|2T}., a quella di un qualunque altro membro.
Polarizzazione e risoluzione spettrale
Nel caso reale in cui T non tende ad infinito, si può mostrare [372]   [372]  Per una determinata frequenza f0, il valore PxT(f0) = |XT(f0)|2T è una variabile aleatoria (dipende infatti da θ), il cui valore atteso mT = Eθ{PxT(f0)} vorremmo fosse pari alla vera densità Px(f0)), e la cui varianza σ2T = Eθ{(PxT(f0) −  Px(f0))2} vorremmo che diminuisse al crescere di T. Per verificare se tali proprietà siano soddisfatte, valutiamo innanzitutto il valore atteso del periodogramma, a partire dalle relazioni fornite dal teorema di Wiener applicato ad XT(f), e cioè |XT(f)|2 = ExT(f) = F {RxT(τ)}:
Eθ{PxT(f)}  =  Eθ⎧⎩F ⎧⎩1T ∞⌠⌡ −∞x(t, θ)rectT(t)x(t + τ, θ)rectT(t + τ)dt⎫⎭⎫⎭ =   =  F ⎧⎩1T ∞⌠⌡ −∞Eθ{x(t, θ)x(t + τ, θ)}rectT(t)rectT(t + τ)dt⎫⎭ =   =  F ⎧⎩Rx(τ)1T ∞⌠⌡ −∞rectT(t)rectT(t + τ)dt⎫⎭ = F {Rx(τ) ⋅ tri2T(τ)} =   =  Px(f) * T( sinc(fT))2
Osserviamo quindi come una finestra di segnale rettangolare ne produca una triangolare sull’autocorrelazione. Ma c’è comunque di buono che all’aumentare di T lo stimatore tende al valore vero, dato che limT → ∞T( sinc(fT))2 tende ad un impulso.
che usando PxT(f) (eq. (10.165)) come una stima ^Px(f) della vera densità Px(f) del processo, si ottiene al suo posto
(10.166) ^Px(f) = Px(f) * T( sinc(fT))2
ossia una distorsione della stessa natura di quella osservato al § 3.8.4 a riguardo del procedimento di finestratura temporale, e che mostra come lo stimatore è polarizzato [373]   [373] Quando il valore atteso di uno stimatore tende al valore vero si dice (vedi § 6.6.3) che lo stimatore è non polarizzato (o unbiased); se poi aumentando la dimensione del campione, la varianza della stima tende a zero, lo stimatore è detto consistente. Ci consola verificare che, come commentato alla nota precedente, per T → ∞ la polarizzazione tende a scomparire, rendendo la stima asintoticamente non polarizzata., e caratterizzato da una risoluzione spettrale [374]   [374] La risoluzione spettrale in questo caso dipende dalla larghezza del lobo principale della densità di energia della funzione finestra applicata a Rx(τ), che nel caso del tri2T(τ) risulta ( sinc(fT))2, il cui lobo principale è appunto ampio 1⁄T. Anche la risoluzione, quindi, migliora all’aumentare di T. (§ 106) dell’ordine di 1⁄T Hz.
Varianza della stima
Come discusso, la stima ^Px(f) tende al vero Px(f) per T che aumenta, migliorando allo stesso tempo il potere di risoluzione in frequenza; d’altra parte però i valori di ^Px(f) per una determinata f sono pur sempre delle v.a., e la loro varianza... non diminuisce all’aumentare di T, rendendo lo stimatore inconsistente! Riprendendo la notazione della nota (372), si può infatti dimostrare [375]   [375] Vedi ad es. http://risorse.dei.polimi.it/dsp/courses/ens_l1/books/libro07secondaparte.pdf che la varianza σ2T della stima (10.165) è pari al valore di Px(f) stesso, ossia per ogni valore di frequenza, la deviazione standard del valore di ^Px(f) è pari a √ Px(f) , indipendentemente da quanto sia grande T. Anche se la teoria prevede che la varianza di uno stimatore diminuisca con l’aumentare dei dati a disposizione (vedi (10.140) a pag. 1), questo non avviene. Il motivo può essere spiegato considerando che in una implementazione numerica mediante dft (§ 4.5), all’aumentare di T aumenta anche il numero di valori in frequenza che sono calcolati, e dunque non si determina un reale accumulo di dati per uno stesso valore stimato. [376]   [376] Esistono diverse soluzioni a questo problema, tutte legate ad una riduzione della risoluzione spettrale. La prima è quella di smussare il ^Px(f) ottenuto, mediando i valori su frequenze vicine: tale operazione corrisponde ad un filtraggio in frequenza. Un secondo metodo prevede di suddividere l’intervallo di osservazione in diversi sottointervalli, calcolare il periodogramma su ciascuno di essi, e mediare i risultati. .
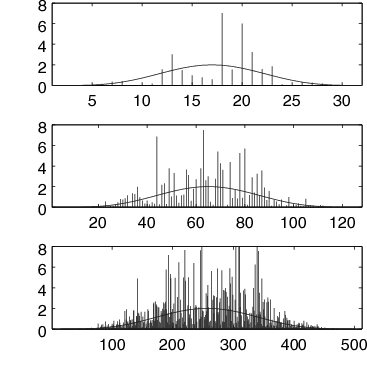
Esempio Approfondiamo il senso di quanto illustrato con l’aiuto di fig. 7.10, in cui mostriamo l’esito del calcolo del periodogramma ottenuto mediante una fft (§ 4.5.2) su di un numero variabile di punti, indicati in ascissa. Sul lato sinistro della figura, il processo x(t, θi) è costituito da un rumore colorato con Px(f) = (1 − cos(4πfTc))2, che pure è mostrato in figura: come anticipato, il valore stimato ^Px(f) si discosta da quello atteso Px(f) in modo tanto maggiore quanto più Px(f) è grande, per qualunque durata di osservazione.
figure f7.1303.png
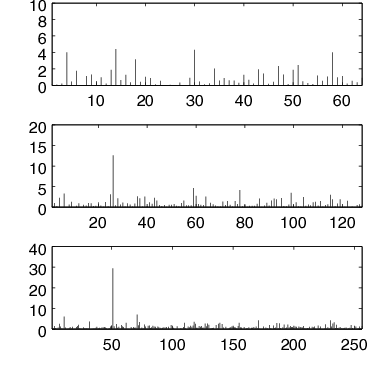
figure f7.1304.png
Figure 7.10 Periodogramma calcolato via FFT per rumore colorato (a sinistra) e per sinusoide immersa nel rumore (a destra), su intervalli di segnale di durata (o numero di punti) crescente (dall’alto in basso)
Viceversa, la colonna di destra di fig. 7.10 mostra l’effettiva utilità del periodogramma per individuare segnali a banda stretta immersi nel rumore. In questo caso una sinusoide con frequenza f0 =  fc 10 e potenza 1 2 è stata sommata ad un rumore gaussiano bianco con σ2n = 4, ottenendo così un SNR pari a 1 8 , ovvero -9 dB. Utilizzando (in alto a destra) una fft a 128 punti (e dunque se ne mostrano la metà, vedi pag. 1), il tono presente appare difficilmente distinguibile dai valori su cui può oscillare la stima per il rumore bianco. Ma è sufficiente raddoppiare (e quadruplicare) il numero di campioni per migliorare la situazione: mentre l’ampiezza della riga alla frequenza della sinusoide raddoppia (ma non la varianza della sua stima), il livello di rumore si mantiene costante (notare la diversa scala orizzontale). Ecco dunque spiegato il motivo del suo nome ☺
 Sezione 7.2: Spettro di densità di potenza Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.4: Filtraggio di segnali e processi