Filtraggio di segnali e processi

Prev Sezione 7.3: Stima spettrale Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.5: Operazioni elementari sui segnali Next

7.4 Filtraggio di segnali e processi

Il teorema di Wiener § 7.2.1 ha fornito un approccio unificato alla definizione di spettro di potenza in virtù del suo legame con la funzione di autocorrelazione per tutti i tipi di segnale, compresi i processi. Riprendiamo quindi l’analisi iniziata al § 3.5.1 estendendola alla classe dei segnali aleatori, per arrivare a descrivere dal punto di vista spettrale e statistico l’uscita di un filtro con risposta impulsiva h(t), ovvero ad y(t) = x(t) * h(t), per i casi di segnale in ingresso di energia, periodico od aleatorio.

7.4.1 Densità spettrale in uscita da un filtro

Valutiamo innanzitutto il risultato per la densità di energia E_y(f) di uscita (e la rispettiva energia E_y) per ingresso di energia, oppure P_y(f) e P_y qualora in ingresso sia presente un segnale x(t) di tipo periodico, di potenza, od un processo.

Segnali di energia

Sappiamo che per il teorema di Parseval risulta E_y(f) = Y(f)Y^*(f); dato poi che Y(f) = X(f)H(f), allora possiamo scrivere

E_y(f) = X(f)H(f) X^*(f)H^*(f) = |X(f)|²|H(f)|² = = E_x(f)|H(f)|²

e dunque la densità di energia dell’uscita è pari al prodotto tra quella in ingresso e |H(f)|². A questo punto, eseguendo l’antitrasformata di Fourier di ambo i membri e ricordando la (10.52), si ottiene:

R_y(τ) = F ⁻¹{E_y(f)} = F ⁻¹{E_x(f)|H(f)|²} = = R_x(τ) * R_h(τ)

ovvero

l’autocorrelazione dell’uscita di un filtro è pari alla convoluzione tra l’autocorrelazione dell’ingresso e quella della risposta impulsiva

Anticipiamo che questo risultato è valido (nei rispettivi termini) anche per i casi di segnale periodico ed aleatorio. Quindi, notiamo che |H(f)|² può essere anche vista come la densità di energia del filtro , ovvero |H(f)|² = E_h(f) = F {R_h(τ)}.

A corollario sussistono le seguenti uguaglianze [377] [377] La quarta uguaglianza sussiste in virtù del teorema di Parseval associato a quello di Wiener, mentre l’ultima è valida se R_H(τ) è reale, ossia se h(t) è idealmente realizzabile e dunque reale, vedi il § 1.6., tutte equivalenti ai fini del calcolo dell’energia totale:

(10.167)
E_y = R_y(0) = ⌠⌡^∞_−∞ E_y(f) df = ⌠⌡^∞_−∞ E_x(f)|H(f)|² df = = ⌠⌡^∞_−∞ R_x(τ)R_h(τ) dτ = ⌠⌡^∞_−∞ R_x(τ)R^*_h(τ) dτ

Segnali periodici

In questo caso il segnale di ingresso x(t) si può esprimere nei termini di una serie di Fourier

x(t) = ⎲⎳_n X_ne^j2πnFt

a cui corrisponde una trasformata X(f) = ∑_nX_n δ(f − nF) (vedi eq. (10.42) a pag. 1) ed una densità di potenza P_x(f) = ∑|X_n|² δ(f − nF) (vedi eq. (10.160)).

Anche il segnale di uscita y(t) è periodico [378] [378] Tenendo conto della natura lineare e permanente del filtro, l’uscita è la combinazione degli effetti degli ingressi, che per un segnale periodico corrispondono alle armoniche., ed i suoi coefficienti di Fourier Y_n possono esprimersi nei termini di quelli dell’ingresso X_n e dei valori della risposta in frequenza (vedi § 3.5.1) come Y_n = X_nH(nF), ovvero in modulo e fase come

|Y_n| = |X_n||H(nF)|; arg(Y_n) = arg(X_n) + arg(H(nF))

Dato che la densità di potenza di y(t) risulta pari a P_y(f) = ∑_n|Y_n|²δ(f − nF), si ottiene

P_y(f) = ⎲⎳|X_n|²|H(nF)|²δ(f − nF) = |H(f)|² P_x(f)

Di nuovo, antitrasformando si ottiene R_y(τ) = R_x(τ) * R_h(τ).

Esercizio

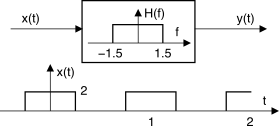
Sia dato il filtro in figura con H(f) = rect₃(f) ed al cui ingresso viene posto il segnale x(t) = 2 ∑^∞_{n = −∞}rect_{1 2}(t − n) Calcolare:

la potenza in ingresso P_x,
la potenza in uscita P_y,
l’espressione di y(t).

Risposte

1) Calcoliamo la media temporale:

P_x = 1 T ∫^T ⁄ 2_{− T ⁄ 2}x²(t)dt = 1 T ∫^1 ⁄ 4_{− 1 ⁄ 4}2²(t)dt = 4 2 = 2

dato che T = 1;

2) Sappiamo che P_y = ∫^∞_−∞P_y(f)df, in cui P_y(f) = P_x(f)|H(f)|², ed essendo x(t) periodico, si ha P_x(f) = ∑_n|X_n|²δ(f − nF). Per determinare i coefficienti della serie X_n, calcoliamo

X(f) = F {2rect_τ(t) * ∑^∞_{n = −∞}δ(t − nT)} = 2τ ⋅ sinc(fτ) 1 T ∑^∞_{n = −∞}δ⎛⎝f − nT⎞⎠

ed essendo τ = 12 e T = 1, risulta

X(f) = sinc⎛⎝f 2 ⎞⎠ ∑^∞_{n = −∞}δ(f − n) = ∑^∞_{n = −∞}X_nδ(f − n)

con X_n = sinc⎛⎝n2⎞⎠. Dunque, dato che gli unici impulsi che cadono entro la risposta in frequenza H(f) sono quelli per f = − 1, 0 e 1, si ha:

P_y(f) = P_x(f)|H(f)|² = ∑¹_n = −1|X_n|²|H(n)|²δ(f − n)

e pertanto si ottiene

P_y = ∫^∞_−∞P_y(f)df = ⎛⎜⎜⎝sin − π2 − π2 ⎞⎟⎟⎠² + 1 + ⎛⎜⎜⎝sinπ2 π2 ⎞⎟⎟⎠² = 1 + 2⎛⎝2 π ⎞⎠² = 1.811

3) Considerando

nuovamente che T = ¹⁄_F = 1, e che risulta X_n = ⎧⎩2 π , 1, 2 π ⎫⎭, si ottiene

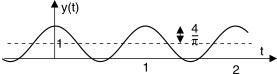
y(t) = ∑¹_n = −1 X_nH(n)e^j2πnt = 1 + 2 π (e^j2πt + e^−j2πt) = 1 + 4 π cos2πt

Notiamo come il filtro lasci passare solamente la componente continua e la prima armonica.

Processi ergodici e segnali di potenza

Anche in questo caso (in appendice 7.7.5) si verifica che m^(1, 1)_Y(τ) = m^(1, 1)_X(τ) * R_h(τ), e dunque

(10.168) P_y(f) = P_x(f)|H(f)|²

Il risultato ovviamente si applica a qualunque membro del processo, per i quali come noto risulta m^(1, 1)_X(τ) = R_x(τ), e dunque la (10.168) è valida anche per un qualunque segnale di potenza.

Esercizio Un processo gaussiano bianco con densità di potenza P_n(f) = N₀ 2 attraversa un filtro causale con h(t) = e^− at. Determinare la P_y(f) in uscita.

Svolgimento Sebbene al § 3.8.8 sia riportato che per questo caso risulta |H(f)|² = 1 a² + 4(πf)² e dunque P_y(f) = P_x(f)|H(f)|² = N₀ 2a² + 8(πf)² , verifichiamo di ottenere lo stesso risultato passando per la R_h(τ), che risulta pari [379] [379] Essendo h(t) reale sappiamo che R_h(τ) è reale pari (pag. 1), dunque è sufficiente calcolarla solamente per τ ≥ 0; inoltre, essendo h(t) = 0 per t < 0 l’estremo inferiore di integrazione parte da zero, ottenendo

R_h(τ)|_τ > 0 = ^∞⌠⌡₀h(t)h(t + τ)dt = ^∞⌠⌡₀ e^− at e^{− a(t + τ)}dt = e^− aτ^∞⌠⌡₀ e^− 2atdt = e^− aτ ⋅ e^− 2at − 2a ||^∞₀ = 1 2a e^− aτ

e dunque R_h(τ) = 1 2a e^− a|τ| a 12a e^− a|τ|, da cui di nuovo otteniamo [380] [380] Tralasciando il termine 12a risulta

F { e^− a|t|} = ^∞⌠⌡_−∞ e^− a|t| e^−j2πftdt = ⁰⌠⌡_−∞ e^{(a − j2πf)t}dt + ^∞⌠⌡₀ e^{− (a + j2πf)t}dt = e^{(a + j2πf)t} a − j2πf ||⁰_−∞ + e^{− (a + j2πf)t} − (a − j2πf)||^∞₀ = 1 a − j2πf + 1 a − j2πf = a + j2πf + a − j2πf (a − j2πf)(a + j2πf) = 2aa² − (j2πf)² = 2a a² + 4(πf)²

|H(f)|² = F {R_h(τ)} = 1a² + 4(πf)².

Guadagno di potenza

E’ il nome con cui viene più spesso indicato (vedi § 255) il rapporto

(10.169) |H(f)|² = P_y(f)P_x(f)

ovvero |H(f)|² = E_y(f) E_x(f) nel caso di segnali di energia. La |H(f)|² ripropone in termini energetici il legame ingresso-uscita rappresentato da H(f) (vedi § 3.5.1). Altre volte |H(f)|² è anche indicato come risposta in potenza, od anche densità spettrale della risposta in potenza, mentre la sua identificazione con la densità di energia del filtro E_h(f) usata a pag. 1 è una mia definizione originale (che io sappia).

7.4.2 Caratteristiche statistiche in uscita da un filtro

Approfondiamo ora lo studio della caratterizzazione statistica dell’uscita di un filtro quando in ingresso è presente un membro di un processo ergodico, per quanto riguarda la media, la varianza, e la d.d.p. del processo in uscita.

Media

è pari a quella dell’ingresso moltiplicata per il guadagno in continua H(0) del filtro, in quanto

m_y = E{y(t)} = E{x(t) * h(t)} = E{x(t)} * h(t) = = m_x^∞⌠⌡_−∞h(τ)dτ = m_xH(0)

Varianza

la condizione di ergodicità consente di scrivere P_y = y²(t) = E{y²} = m⁽²⁾_y e dunque, ricordando l’eq. (10.119), si ha

σ²_y = m⁽²⁾_y − (m_y)² = P_y − (m_y)²

in cui per valutare P_y si può far uso di relazioni analoghe alle (10.167):

P_y = R_y(0) = ^∞⌠⌡_−∞ P_y(f)df = ^∞⌠⌡_−∞P_x(f)|H(f)|²df = = ^∞⌠⌡_−∞R_x(τ)R_h(τ)dτ

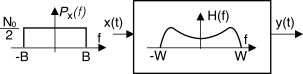
Esempio In ingresso ad un filtro

H(f) viene posto un processo x(t) bianco con m_x = 0 e banda B, ovvero P_x(f) = N₀2 rect_2B(f) e quindi R_x(τ) = N₀B ⋅ sinc(2Bt). Essendo il processo a media nulla, per la varianza di uscita si ottiene

σ²_y = P_y = ^∞⌠⌡_−∞P_x(f)|H(f)|²df = N₀ 2 ^B⌠⌡_− B|H(f)|²df ≤ N₀ 2 R_h(0)

con il segno di uguale se la larghezza di banda W di H(f) è minore di B [381] [381] Infatti in tal caso ∫^W_− W|H(f)|²df è proprio pari all’energia della h(t); se viceversa W > B una parte di |H(f)|² cade al di fuori degli estremi di integrazione ( − B, B), e non contribuisce al risultato.. Per quanto riguarda la densità spettrale di potenza P_y(f) di uscita si applica la (10.168), ottenendo P_y(f) = P_x(f)|H(f)|² = N₀ 2 |H(f)|² con |f| ≤ B: dunque il relativo processo y(t) di uscita non è più bianco, ed in questo caso si dice colorato. A ciò corrisponde anche una modifica della funzione di autocorrelazione, che non è più un sinc, ma ora vale

R_y(τ) = R_x(τ) * R_h(τ) = N₀B ⋅ sinc(2Bt) * R_h(τ)

Ciò significa che mentre prima del filtro (per il processo bianco) due valori estratti in istanti multipli di ¹⁄_2B erano incorrelati, l’operazione di filtraggio ha introdotto un legame tra i valori estratti a tali intervalli [382] [382] Questo risultato può essere analizzato ricordando che l’integrale di convoluzione calcola i singoli valori in uscita da un filtro, come dipendenti da tutti gli ingressi passati, ognuno pesato con il valore della risposta impulsiva relativo al ritardo tra ingresso passato ed uscita presente (vedi § 3.4.3). Pertanto, anche se i singoli valori in ingresso sono statisticamente indipendenti, quelli di uscita (distanti tra loro per meno della durata della risposta impulsiva) condividono una porzione di storia comune, e quindi i loro valori non sono più incorrelati..

Densità di probabilità

A riguardo della p_Y(y) del processo di uscita non si può dire nulla di generale, tranne che evidentemente dipende dalla p_X(x) di ingresso e dalle operazioni compiute dal filtro; la sua espressione esatta va però determinata di volta in volta. Ad esempio, nel caso di un filtro trasversale (§ 5.2.1) possono applicarsi le regole di cambio variabile (§ 6.4). Un caso a parte è quello dei processi gaussiani, che se posti in ingresso ad un filtro, producono in uscita un processo anch’esso gaussiano [383] [383] Questo risultato è una diretta conseguenza della proprietà di invarianza dei processi gaussiani rispetto alle trasformazioni lineari discussa al § 6.5.2. Infatti, riscrivendo l’operazione di convoluzione y(t) = ∫x(τ)h(t − τ)dτ in forma approssimata come una somma di infiniti termini y(t) = ∑_ix(τ_i)h(t − τ_i)Δτ_i appare evidente come, nel caso in cui x(t) sia un processo gaussiano, l’uscita sia costituita da una combinazione lineare di v.a. gaussiane, e dunque anch’essa gaussiana..

Prev Sezione 7.3: Stima spettrale Su Capitolo 7: Correlazione, densità spettrale e filtraggio Sezione 7.5: Operazioni elementari sui segnali Next